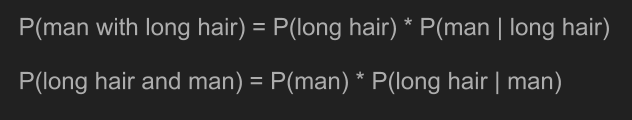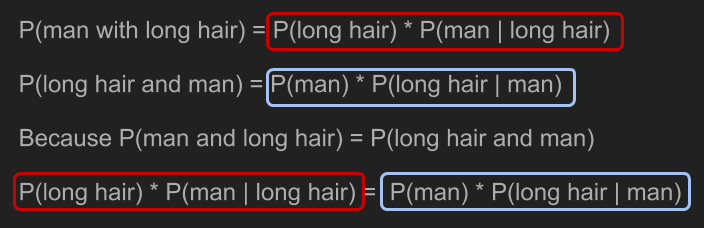贝叶斯推断的运作原理

原文：How Bayesian inference works

Translated from Brandon Rohrer's Blog by Jimmy Lin

• Google 演示文稿上的投影片

贝叶斯推断（Bayesian Inference）是一套可以用来精进预测的方法，在数据不是很多、又想尽量发挥预测能力时特别有用。

虽然有些人会抱着敬畏的心情看待贝叶斯推断，但它其实一点也不神奇或神秘，而且撇开背后的数学运算，理解其原理完全没有问题。简单来说，贝叶斯推断可以帮助你根据数据，集成相关信息，并下更强的结论。

「贝叶斯推断」取名自一位大约三百年前的伦敦长老会（Presbyterian）牧师——汤玛士．贝叶斯（Thomas Bayes）。他写过两本书，一本和神学有关，另一本和统计学有关，其中包含了当今有名的贝氏定理（Bayes Theorem）的雏形。这个定理之后被广泛应用于推断问题，即用来做出有根据的推测。如今，贝叶斯的诸多想法之所以会这么热门，另一位主教理乍得·普莱斯（Richard Price）也功不可没。他发现了这些想法的重要性，并改进和发表了它们。考虑到这些历史因素，更精确一点地说，贝氏定理应该被称作「贝叶斯－普莱斯规则」。

电影院里的贝叶斯推断

请读者先想像你人在电影院，刚好看到前面有个人掉了电影票。这个人的背影如上图所示，你想叫住他／她，但你只知道这个人有一头飘逸长发，却不知道他／她的性别。问题来了：你该大喊「先生，不好意思」还是「女士，不好意思」？根据读者对两性头发长度的印象，你或许会认为这个人是女的。（在这个简单的例子里，我们只考虑长发和短发、男性和女性。）

但现在考虑另一个状况：如果这个人排在男性洗手间的队伍当中呢？多了这项信息，读者或许会认为这个人是男的。我们可以不经思索地根据不同的常识和知识调整判断，而贝叶斯推断正是将这点化为数学，帮助我们做出更精准的评估。

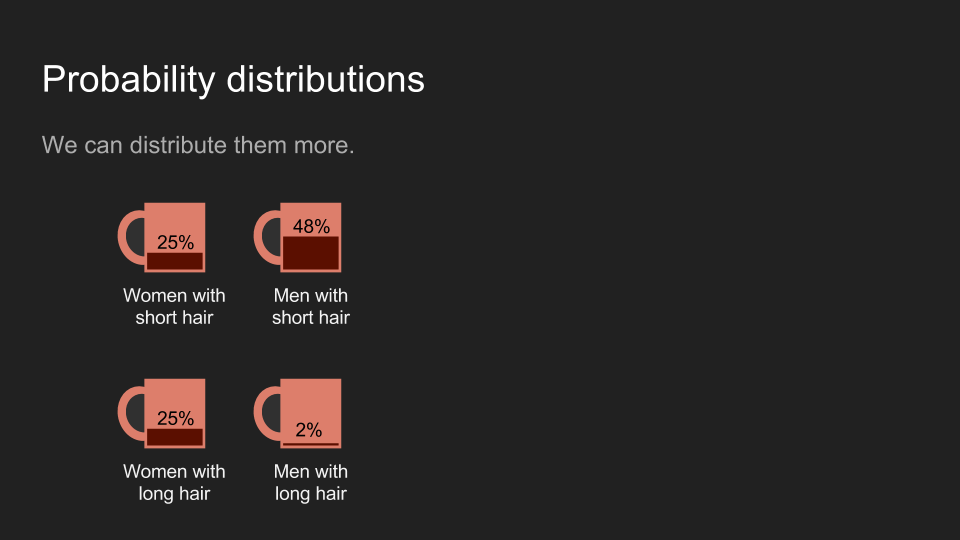
为了将前面的例子用数学表达，我们可以先假设电影院里的人有一半是女的，有一半是男的。也就是说 100 个人里面，有 50 名男性和 50 名女性。在这 50 名女性里，有一半的人有长发（25 人），另一半有短发（25 人）；在 50 名男性当中，48 个人有短发，两个人有长发。因为在 27 位长发观众里，有 25 位是女性和两位男性，所以前面第一个猜测很安全。

但如果我们换一个场景：在男性洗手间队伍的 100 个人里面，有 98 位男性和两位陪伴中的女性。这里的女性虽然也有一半是长发、一半是短发，但人数减为一位长发女性和一位短发女性。男性观众中长发和短发的比例也不变，不过因为总人数变成了 98 人，现在队伍里有 94 位短发男性，和四位长发男性。由于现在长发观众中有一名女性和四名男性，保守的猜测变成了男性。从这个例子，我们可以很容易地理解贝叶斯推断的原理。根据不同的先决条件——也就是这名观众是否站在男性洗手间的队伍里，我们可以做出更准确的评估。

为了好好说明贝叶斯推断，我们最好先花点时间清楚定义一些观念。很不凑巧这段会用到一些数学，不过我们会避免谈任何不必要的细节，请读者务必耐心读完以下几段，这对理解之后的内容很有帮助。为了打好基础，我们需要快速认识四个观念：机率（probabilities）、条件机率（conditional probabilities）、联合机率（joint probabilities）和边际机率（marginal probabilities）。

机率

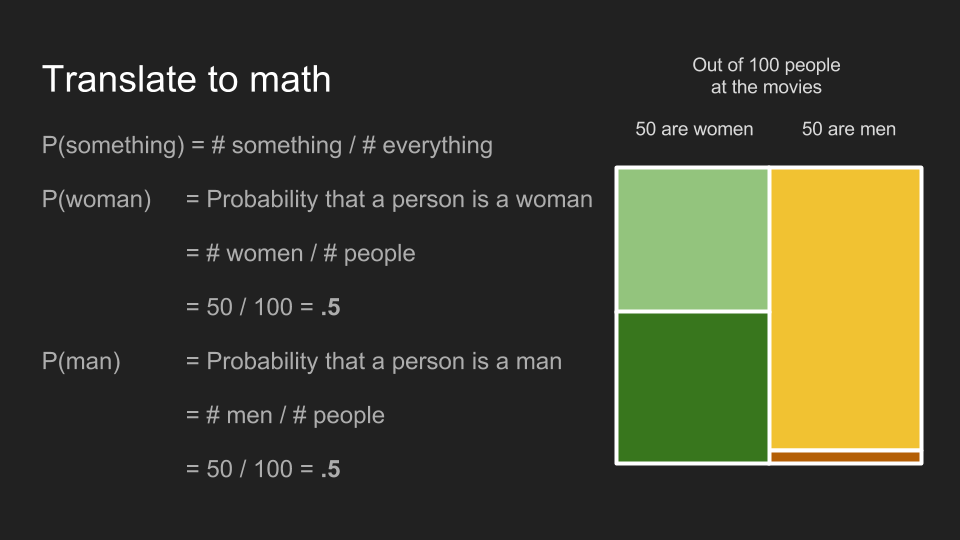
某事件发生的机率，就是将「该事件的数量」除以「所有可能发生的事件数量」。在我们的例子里，某位观众是女性的机率是 50 名女性除以 100 位观众，即 0.5 或 50%。观众是男性的机率也是 50%。

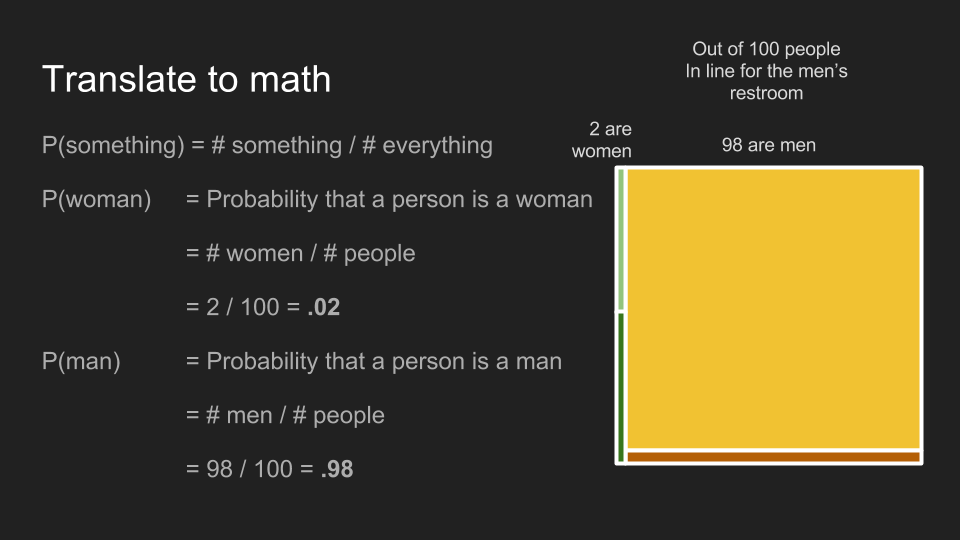
在男性洗手间的队伍里，观众是女性的机率为 0.02，男性的机率为 0.98。

条件机率

条件机率所能回答的问题是「如果这名观众是女性，那她有长头发的机率为何？」条件机率的计算方式和一般机率相同，只不过条件机率只会涉及符合条件的少部分样本。在我们的例子里，女性观众中有长发的条件机率 $P(long \space hair | woman)$ 即「长发女性人数」除以「女性总人数」，也就是 0.5。不管我们是计算电影院里的观众，还是男性厕所队伍里的观众，都会得到相同的条件机率。

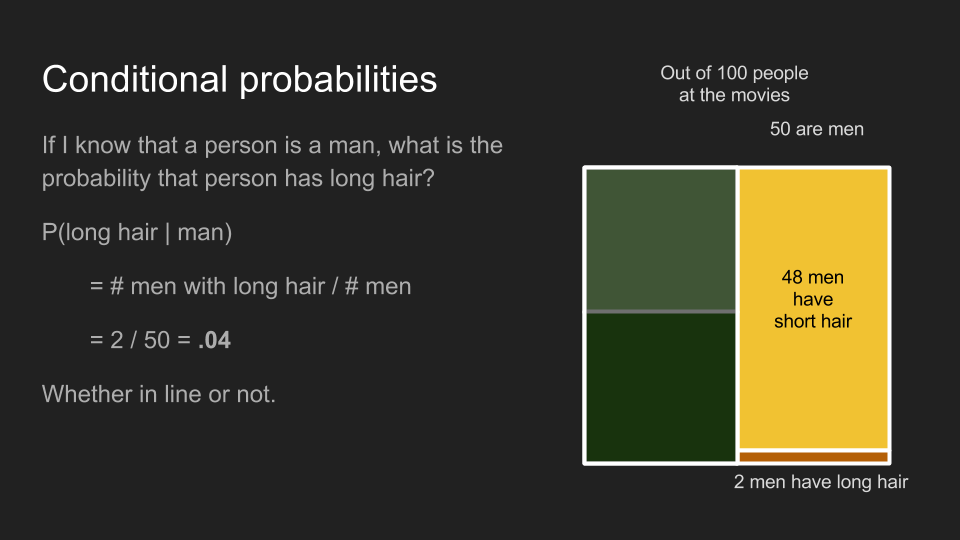
运用相同的方法，男性观众中有有长发的条件机率 $P(long \space hair | man)$ 为 0.04，不管是队伍里还是队伍外的男性。

关于条件机率，有一件需要特别注意的事：$P(A | B)$ 并不等于 $P(B | A)$。例如 $P (cute | puppy)$ 并不等于 $P (puppy | cute)$。如果我手上抱着的东西是一只狗狗，那这个东西很可爱的机率就很高，但如果我只知道我手上抱着的东西很可爱，那这个东西是狗狗的机率只有中下，因为它也有可能是猫猫、兔兔、小刺猬或小婴儿。

联合机率

联合机率适合用来回答这类问题：「这位观众是一名短发女性的机率为何？」回答这个问题的过程分为两个步骤。首先，我们会先找出观众是女性的机率 $P(woman)$；接着，我们再找出在女性观众中短发的条件机率 $P(short \space hair | woman)$。将两个机率相乘，就可以得到前面问题所求的联合机率，即 $P(woman \space with \space short \space hair) = P(woman) * P(short \space hair | woman)$。利用这个方法，我们可以重算一次之前的结论——电影院里，某位观众为长发女性的机率 $P(woman \space with \space long \space hair)$ 为 0.25，但男性洗手间的队伍里，某位观众为长发女性的机率 $P(woman \space with \space long \space hair)$ 为 0.01。两者之所以不同，是因为观众为女性的机率 $P(woman)$ 在两个情况下不同。

同理，我们也可以算出电影院里，某位观众为长发男性的联合机率 $P(man \space with \space long \space hair)$ 为 0.02，但在男性洗手间队伍里的联合机率则为 0.04。

联合机率和条件机率不同的地方，在于联合机率的计算顺序并不影响结果。也就是说 $P(A \space and \space B)$ 和 $P(B \space and \space A)$ 是一样的。我喝牛奶又吃果酱甜甜圈（jelly donut）的机率，和我吃果酱甜甜圈又喝牛奶的机率是一样的。

边际机率

最后，我们需要了解的是边际机率，它可以用来回答这类问题：「某位观众有长发的机率为何？」要回答这个问题，我们需要将所有符合这个条件的事件发生机率加总——即长发男性和长发女性的联合机率。将这两个联合机率相加以后，我们可以得出在电影院里的观众是长头发的机率 $P(long \space hair)$ 为 0.27，但在男性洗手间的队伍里这个机率只有 0.05。

贝氏定理

介绍完四个重要的观念以后，终于可以来谈我们关心的问题了。我们想要了解「如果我们知道某人有长头发，这个人是女性（或男性）的机率为何？」这也是条件机率 $P(man | long \space hair)$ 的解，但我们现在只知道顺序相反的情况 $P(long \space hair | man)$，即「如果我们知道某人是男性，这个人有长头发的机率为何？」因为条件机率的顺序不可任意调换，我们还没办法回答这个问题。

幸好汤玛士．贝叶斯早就发现了一个可以为我们解答的神奇工具。

根据联合机率的计算方法，我们可以将前面两个条件机率写成「男性且长发」$P(man \space with \space long \space hair)$ 和「长发且男性」$P(long \space hair \space and \space man)$ 的计算式。由于联合机率的顺序是可以互换的，两者完全相同。

利用一点代数计算，我们就能解决前面的问题，即求出 $P(man | long \space hair)$。

将「长发」和「男性」以 A 和 B 代换，我们就得到了贝氏定理。

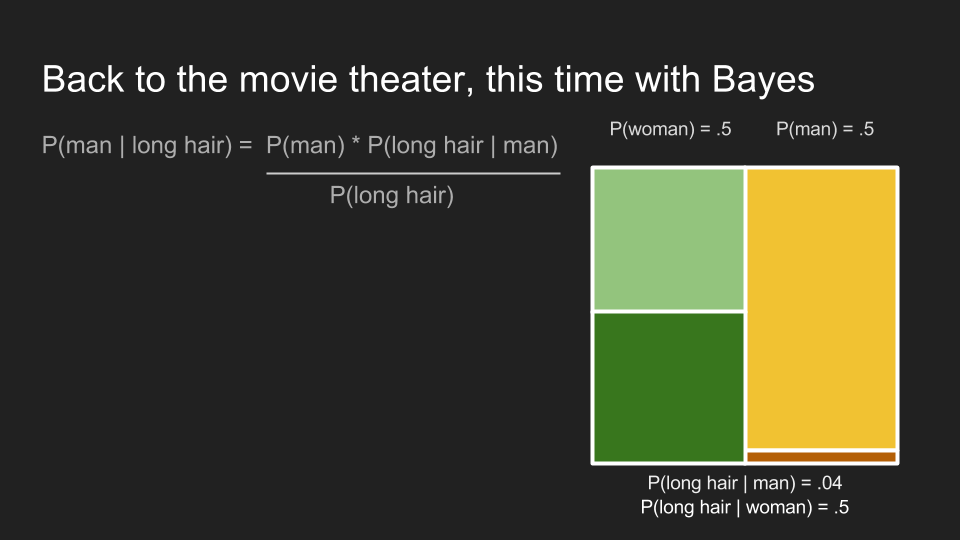
最后我们终于可以解决前面的电影票问题了。这里我们可以应用贝氏定理。

首先，我们需要求出长发观众的边际机率，$P(long \space hair)$。

接下来，我们可以代入前面的数字，并算出长发观众为男性的机率。在男性洗手间的队伍里，该机率 $P(man | long \space hair)$ 为 0.8。这印证了我们先前认为长发观众应该为男性的直觉。也就是说，贝氏定理印证了我们在该情况下的直觉。更重要的是它融合了我们对男性队伍中，男性人数远大于女性的既有信息。利用这项信息，贝氏定理更新了我们在该状况下的信念（belief）。

机率分布

虽然电影院这类的例子，已经足以说明贝叶斯推断的重要性和运作原理，但在数据科学的应用中，贝叶斯推断最重要的功用是用来解释数据。在拥有少量数据的情况下，我们可以借着融入问题的背景知识以做出更强的结论。这点我会再详细说明，但请先容许我再多介绍一个概念——我们需要先弄清楚机率分布（probability distributions）到底是什么。

读者可以先将机率想成一壶刚好可以倒满一个杯子的咖啡。如果我们只有一个杯子，那就没什么需要讨论的问题了；但如果我们有很多杯子，我们就需要决定要给每个杯子倒多少咖啡。读者可以任意决定咖啡的量，只要将咖啡倒完就好。在刚才的电影院问题里，我们可以将男性和女性比喻为杯子。

我们也可以用四个杯子比喻两个性别和两种头发长度的组合。不管比喻为何，全部咖啡加总都应该是一个杯子的量。

一般来说，我们会将这些杯子排成一排，这时咖啡的量可以看作是一张直方图（histogram）。我们可以将咖啡想成我们的信念（belief），并将咖啡在不同杯子里的分布，想成对不同的结果的信念强烈程度。

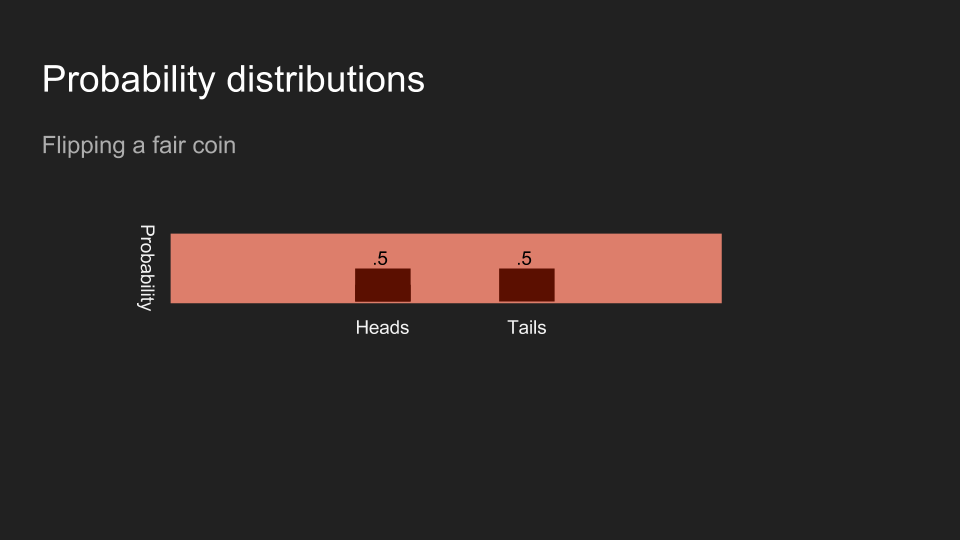
如果我掷一枚硬币，而且不让读者看到结果，读者对硬币正反面的信念应该是一半一半。

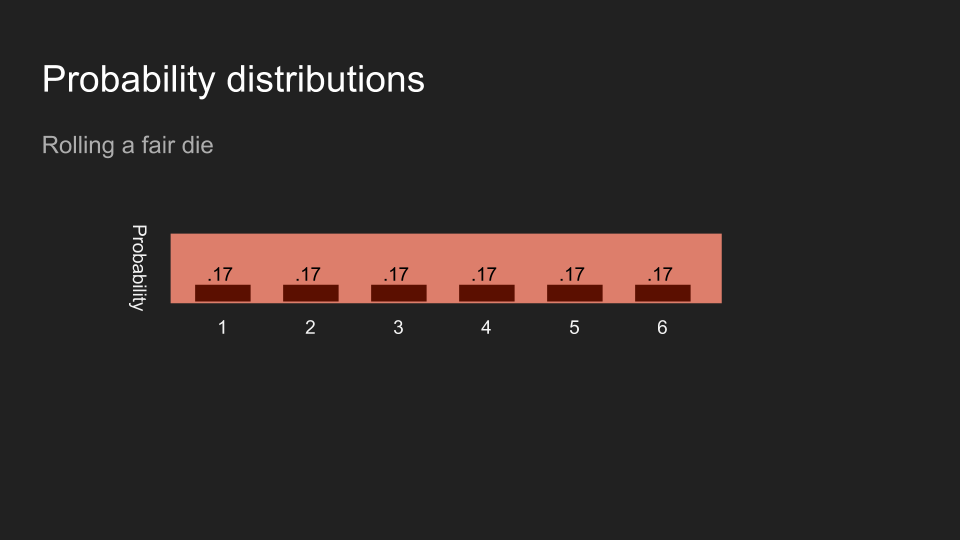
如果我丢一个骰子，而且不让读者看到结果，读者对骰子正面数字的信念应该会平均分布于六个数字。

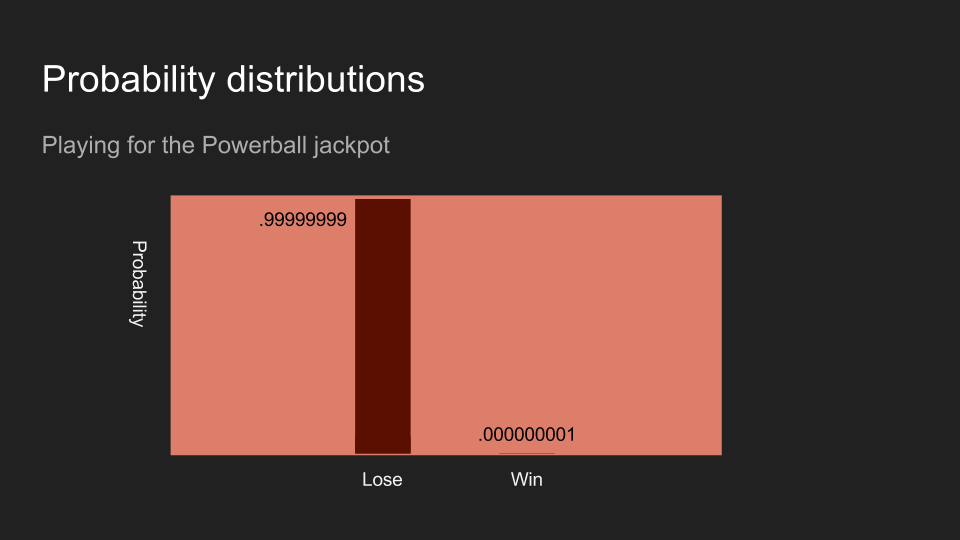
如果我买了一张彩券，读者对赢得彩券的信念应该会趋近于零。以上三个例子：掷硬币、丢骰子、和买彩券，都是数据测量和收集的例子。

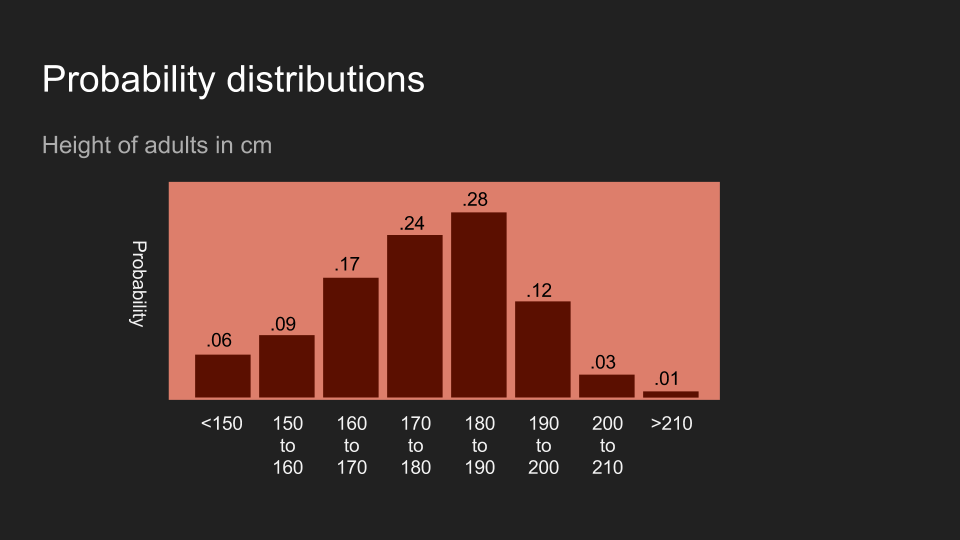
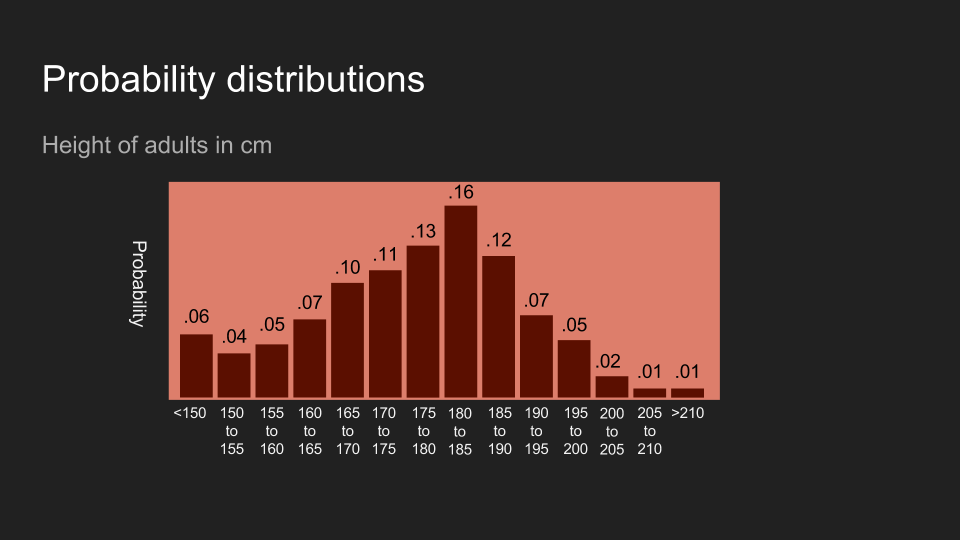
不意外地，读者也可以对其它形式的数据抱持着一定的信念。以美国成人的身高为例，如果我说我刚量完某人的身高，读者的信念可能会和上面的图片类似。这代表读者相信这个人的身高应该介于 150 到 200 公分，而且最有可能介于 180 和 190 公分。

我们还可以将分布中的群类（bin）分得更细。读者可以把这想成将咖啡分到更多杯子中，每个杯子分的咖啡更少，信念的分布也更细致。

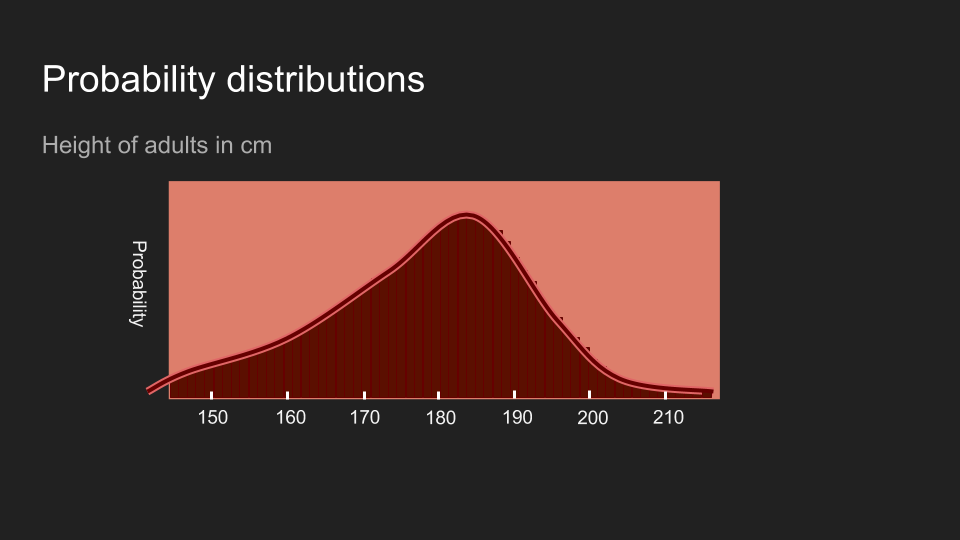
等杯子数量多到一个程度以后，我们就不太能用杯子来比喻了。在这个情况下，机率的分布变得连续，需要不同的计算方法，但是背后的概念还是很管用：机率分布反映了信念的分布。

感谢读者的耐心。在介绍完了机率分布以后，我们可以利用贝叶斯推断来解读数据了。为了说明整个流程，我们来量一下我的狗狗的体重。

兽医院里的贝叶斯推断

我的狗狗名叫阿怖（Reign of Terror）。当我带她去看兽医时，她会在体重计上扭来扭去，这让量体重变成一件很困难的事。但是了解精确的体重很重要，因为如果她变重了，我们就得减少阿怖的食物量。由于阿怖把食物看得比自己的命还重，量好体重真的很重要。

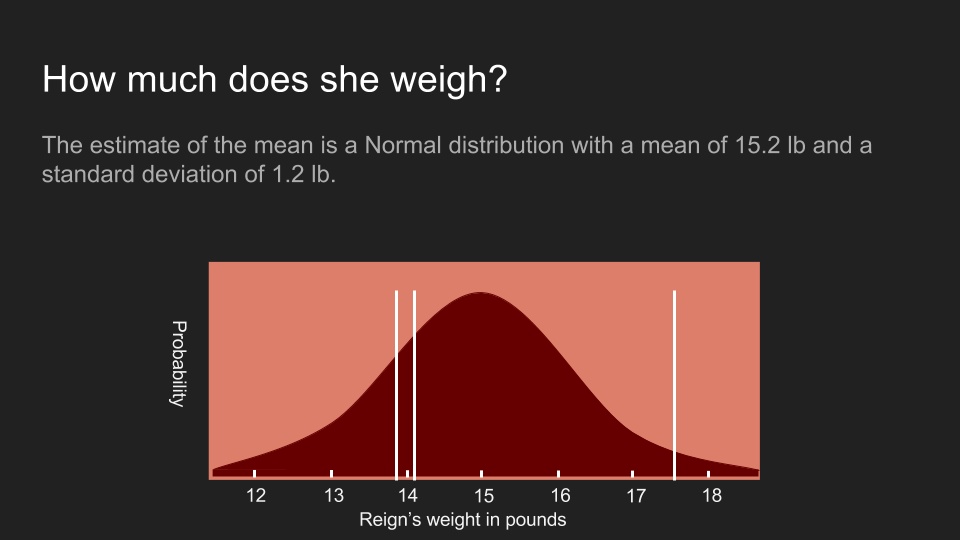
我们上次去看兽医的时候，在阿怖变得无理取闹之前兽医量到了三个体重：13.9 磅、17.5 磅和 14.1 磅（翻注：一磅约等于 0.45 公斤）。我们可以按一套标准的统计方法，将这些数据化为机率分布。我们可以先计算这组数据的平均值、标准差（standard deviation）和标准误差（standard error），再创建一套阿怖的体重分布。

根据这个方法所得出的分布，显示了我们对阿怖体重的信念。阿怖的体重呈常态分布（normal distributed），有着 15.2 磅的平均值，以及 1.2 磅的标准误差。图上的白线是我们实际测量到的三个数值。不过很不凑巧地，这个分布曲线有点太宽了。虽然最大值位于 15.2 磅，但这个机率分布显示阿怖的体重还是很有可能低于 13 磅或超出 17 磅。在这么宽的范围里，我们很难做出任何确切的决定。通常我们遇到这种情况时，会选择回去收集更多数据，但有时这么做不太可行或成本很高。在我们的例子里，阿怖已经失去了耐心，所以我们只能利用这三组数值。

这时贝氏定理就派上用场了。贝氏定理很适合用来充分利用少量数据。在实际应用之前，我们可以先来回顾一下贝氏定理的算式和每个部分。

我们先将算式中的 A 和 B 换成体重（w，weight）和测量结果（m，measurement），以便说明如何使用贝氏定理。图片中的四个部分分别代表不同的处理步骤。

首先，事前机率（prior probability）$P(w)$ 代表我们的事前信念。在这个例子里，事前机率就是我们在将阿怖放上体重计前，对她体重分布的信念。

算式中的概似机率（likelihood）$P(m | w)$ 代表在某个既定体重下，我们得到这些测量结果的机率。这也被称作数据的概似机率（the likelihood of the data）。

事后机率（posterior probability）$P(w | m)$ 则代表在某测量值出现的情况下，阿布实际体重为 $w$ 的机率。这也是我们最关心的部分。

最后，数据机率（probability of data）$P(m)$ 代表我们得到某测量值的机率。在这个例子里，我们就假设这是一个常数，即体重计本身没有误差。

我们可以先放心抛开所有假设，当作自己完全不知道任何状况。也就是说在这个例子里，我们可以假设阿怖的体重为 13 磅、15 磅、一磅甚至一百万磅的机率完全相等，让数据说话。为了做到这点，我们假设事前机率为均匀分布（uniform distribution），即任何体重发生的机率都是一个固定的常数。这可以帮助我们将贝氏定理简化为 $P(w | m) = P(m | w)$。

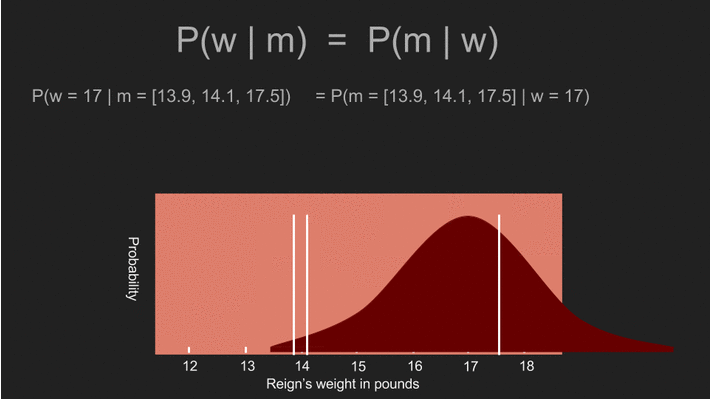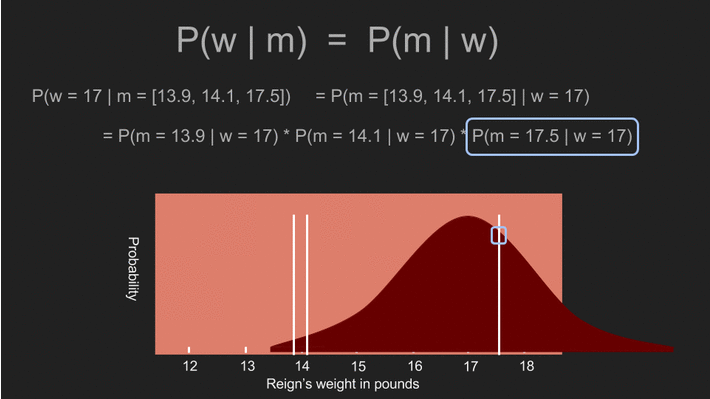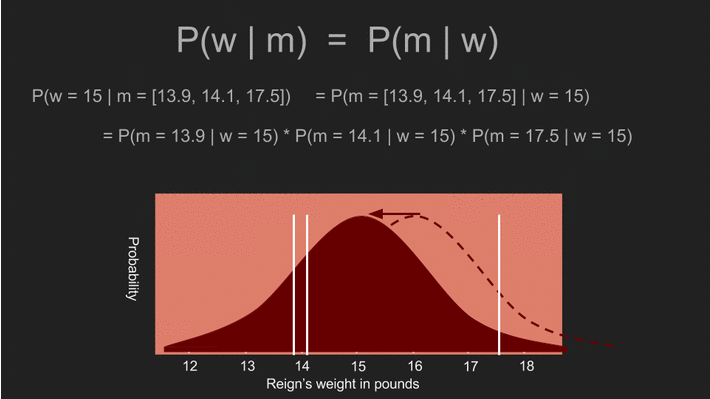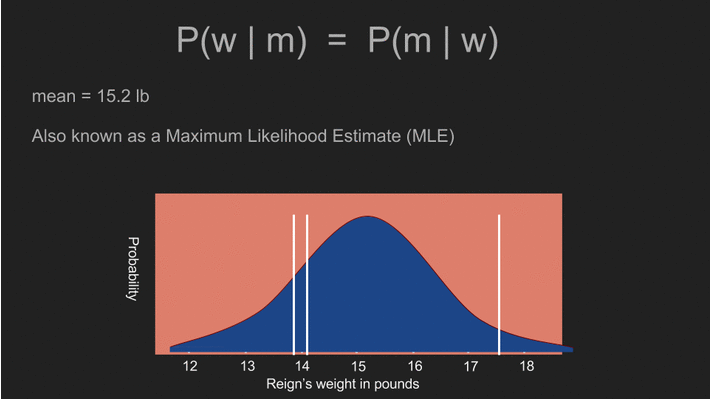
现在我们用阿怖所有可能的体重来计算得到这三组测量值的概似机率。例如，如果阿怖的体重是一千磅，那我们得到这三组测量值的机率应该是微乎其微。但如果阿怖的体重介于 14 到 16 磅之间，这三组测量值出现的机率就很高。我们可以利用不同的体重，重复计算得到特定测量值的机率，即 $P(m | w)$。由于我们假设事前机率为均匀分布，这也是事后机率 $P(w | m)$ 的估计值。

这么做所得到的答案，会和前面利用平均值、标准差和标准误差所算出的答案非常相似。实际上，两个答案确实完全一模一样，因为利用均匀分布的事前机率，就会得到传统统计方法下的估计值。机率分布曲线中的最高点，即平均值 15.2 磅，也被称为阿怖体重的最大似然估计值（maximum likelihood estimate，MLE）。

虽然我们利用了贝氏定理，但我们还没得到真正有用的估计值。为了达成这个目的，我们需要一个非均匀分布的事前机率。事前机率代表在测量前我们对某件事物的信念，而一个均匀分布的事前机率，则代表我们认为任何结果发生的机率都一样。但这种情况其实不常见，因为我们通常对于测量的事物本身都有一定的认识。比方说，年龄永远只会大于零、气温永远比摄氏 -276 度还高、成人的身高很少超过八英尺（约 244 公分）。我们通常能运用一些相关的领域知识（domain knowledge）得知哪些情况发生的机率比较高。

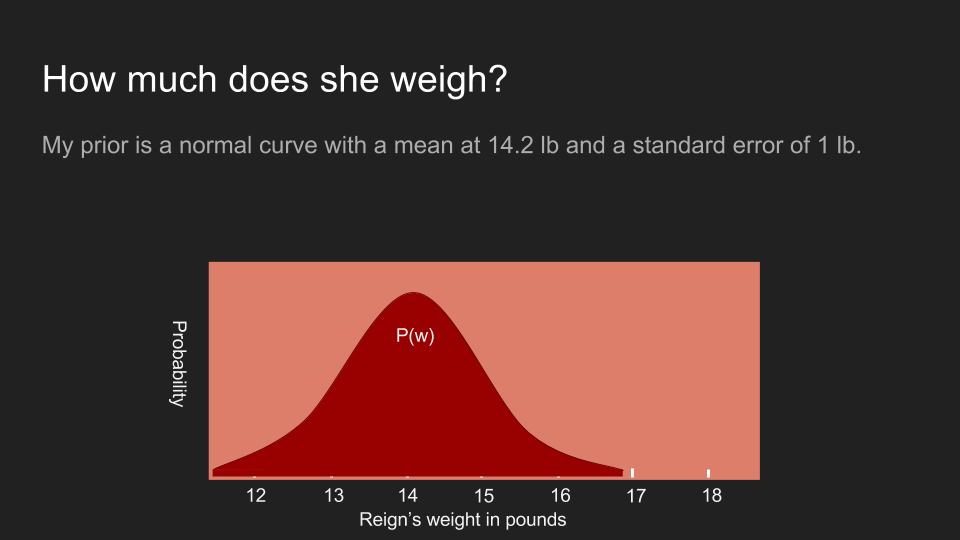
所以在阿怖的例子里，我确实有一些相关信息。我知道上次我们来看兽医的时候，阿怖的体重是 14.2 磅。而且我最近并没有感觉阿怖变得特别重或轻，尽管我的手臂不如体重计灵敏。因此，我相信阿怖的体重应该在 14.2 磅附近，有可能变轻或变重一两磅。为了呈现这个信念，我建构了一个平均为 14.2 磅、标准差为 0.5 磅的正态分布。

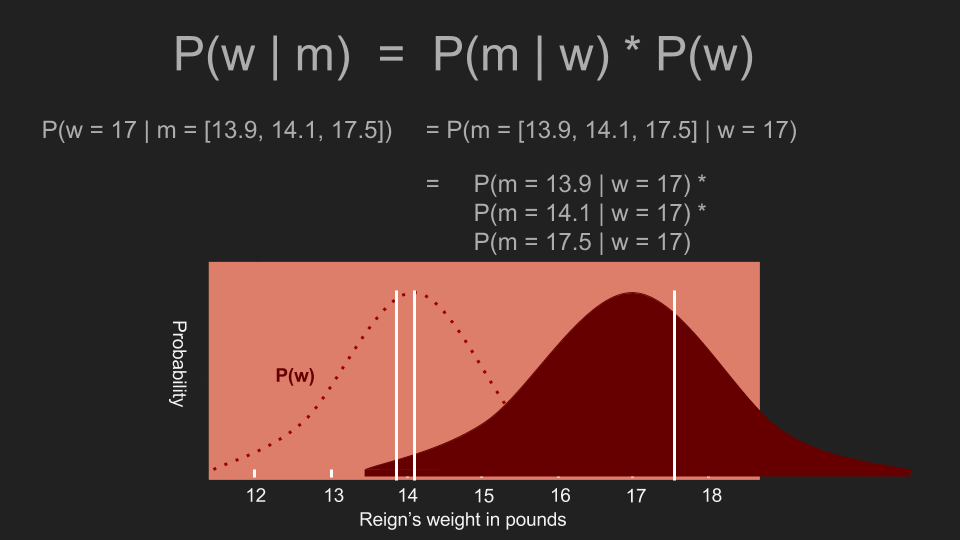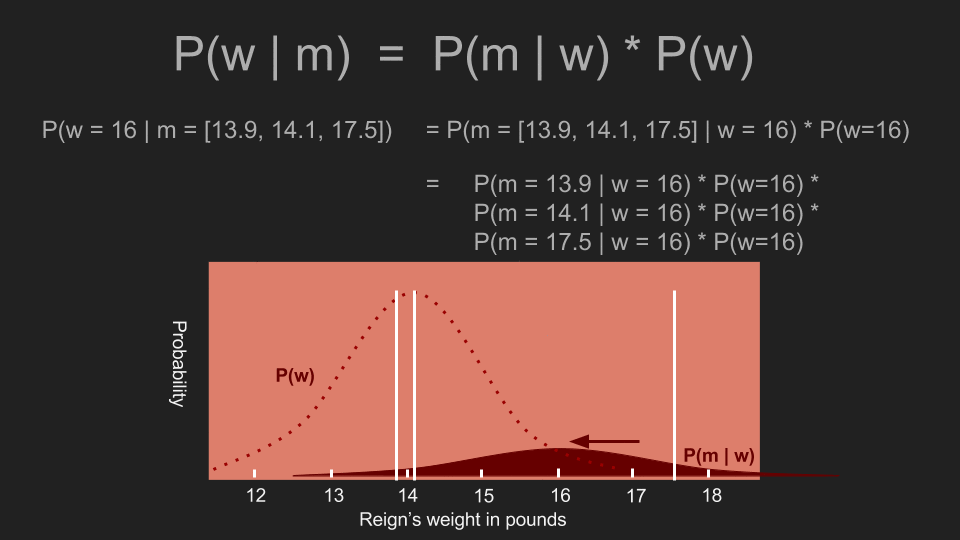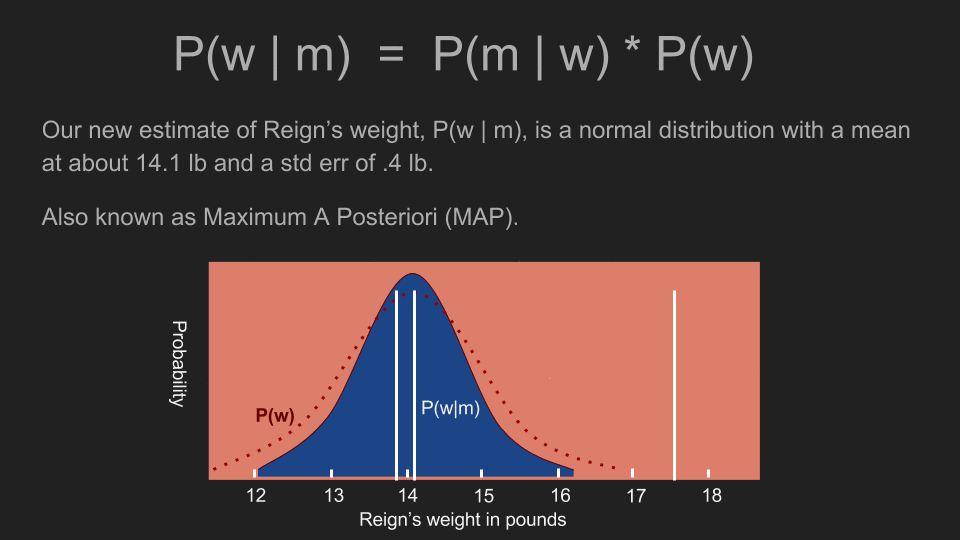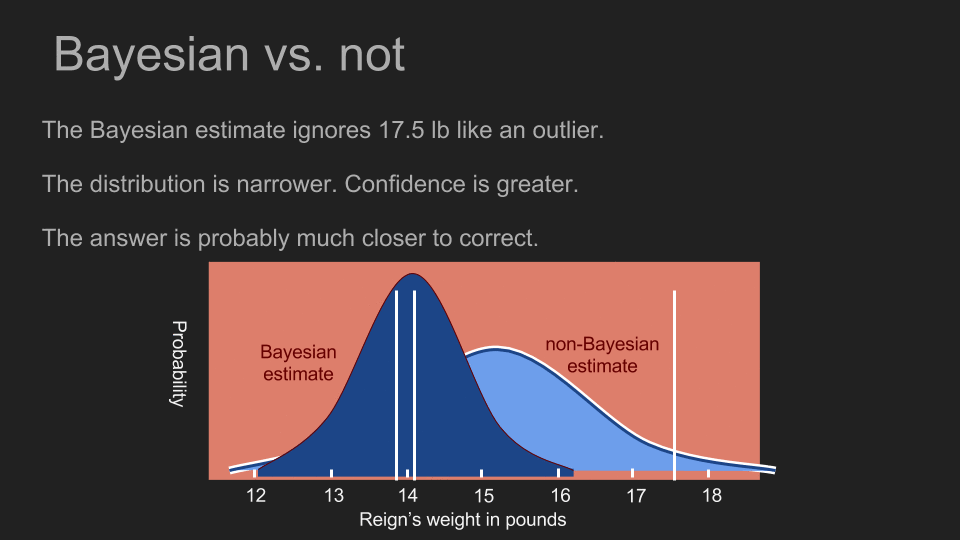
有了这个事前机率后，我们可以重复以上事后机率的计算步骤。为了计算事后机率，我们先计算阿怖体重为一个特定值（例如 17 磅）的机率，再将「（根据事前机率，）阿怖的体重确实是 17 磅的机率」和「在阿怖体重是 17 磅的情况下，得到这些测量值的条件机率」相乘。接着我们可以利用这个方法测试各种可能的体重，这时事前机率所扮演的角色，是压低或放大某些体重发生的机率。在我们的例子里，事前机率会为 13 到 15 磅的估计值赋予更多权重，并削弱这个范围外的权重。这正是采用正态分布和均匀分布之间的差异。在均匀分布的事前机率下，即使是 17 磅的估计值都还有不错的发生机率；但在正态分布的事前机率下，它的发生机率已经处于分布的尾端了。乘上事前机率会使 17 磅发生的机率变得非常低。

在计算完每个体重的发生机率以后，我们就有了一个新的事后机率分布。这个分布曲线的最高点被称为最大后验机率（maximum a posteriori estimate，MAP），在这个例子里为 14.1 磅。这和我们之前利用均匀事前机率所算出的最高点（15.2 磅）差很多。新的高峰也更陡峭，这代表我们可以对这个估计值抱持更高的信心。现在我们可以看出阿怖的体重并没有什么变化，她的食物量也不需要增减。

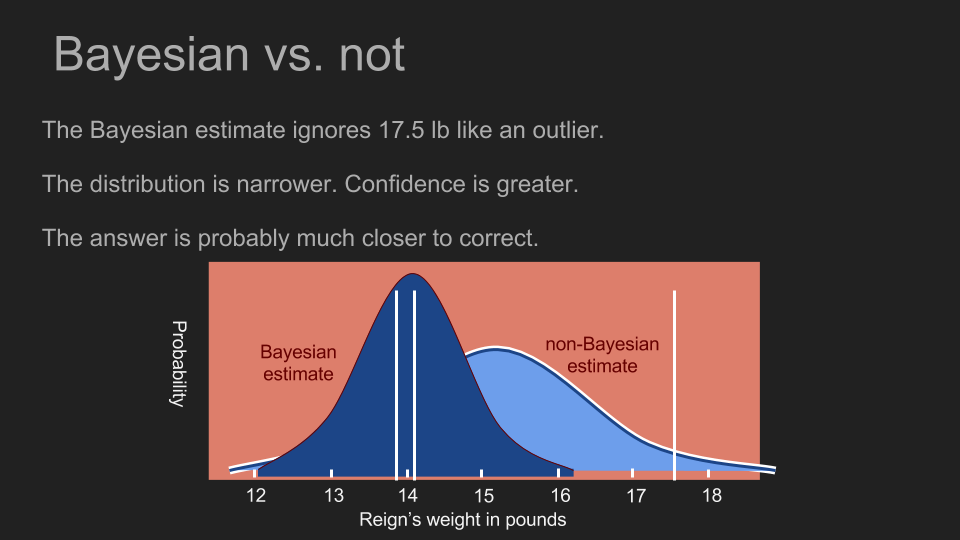
借由融合我们对测量目标已知的信息，我们可以做出更精准、更有信心的估计，也能帮助我们善用少量数据。当我们所采取的事前分布，对 17.5 磅的测量值赋予很低的发生机率时，这几乎等同于将 17.5 磅当作异常值拒绝。不过我们并不需要凭直觉或知识判断异常值；贝氏定理可以帮助我们运用数学，解决这个问题。

直得留意的是，在阿怖的例子里，我们直接假设得到某测量值的机率 $P(m)$ 为均匀分布。但如果我们得知体重计有一定的偏差，也可以将这项信息融入 $P(m)$ 当中。如果这个体重计只会显示偶数、有 10% 的机率会显示 2.0 磅、或是每用三次就会跳出随机的测量值，我们也可以借由修改 $P(m)$ 反映这些现象、精进事后机率。

避免贝氏陷阱

虽然在阿怖的例子里，我们学到了使用贝氏推断的好处，但同时也该留意潜在的陷阱。我们虽然能借由对答案作出假设，以提升估计的精确程度，但测量、估计某事物的目的，终究在于更加了解该事物。如果我们认为自己已经知道答案，那这么做可能反倒是在修正数据。马克．吐温（Mark Twain）对此有很精辟的见解：「让我们陷入困境的不是无知，而是信以为真的谬误。」

如果我们一开始就武断地认为阿怖的体重应该介于 13 到 15 磅，那我们可能永远都不会发现，她的体重其实已经掉到 12.5 磅了。因为不管我们测量多少次，我们所采用的事前分布都会对 12.5 磅赋予 0% 发生机率，也会忽略所有低于 13 磅的测量值。

幸好有一个方法可以帮助我们规避这个风险：只要至少给每个结果分配一点机率，我们就可以避免盲目地消去任何可能性。如此一来，就算世事难料，阿怖长成了一千磅，我们所得到的测量值也还是能反映在事后机率上。这就是为什么正态分布很常被用作事前机率的模型，它一方面可以集中我们对小范围结果的信念，一方面具有即使无限延伸，机率也永不归零的长尾。

在这段对话中，红心皇后就是一个很好的典范：

爱丽丝笑了，说：「试也没用，一个人不能相信不可能的事。」

「我敢说这是妳练习得不够，」王后说，「我像妳这样大的时候，每天练上半小时呢。嘿！有时候，我吃早饭前就能相信六件不可能的事哩！」

——路易斯．卡罗（Lewis Carroll）《爱丽丝梦游仙境》

修正：感谢发现错字和错误的读者们！Justin Fortier 和 Irina Max，我欠你们一杯饮料。

Brandon，于 2016 年 11 月 2 日

译注

1. 《爱丽丝梦游仙境》节录的中文翻译引自黄盛《飞越爱丽丝：逻辑、语言和哲学》。