線性迴歸的運作原理
原文連結:How linear regression works
Translated from Brandon Rohrer's Blog by Jimmy Lin
線性迴歸(linear regression)是在資料點中找出規律、畫出一條直線的專業說法,以下我將透過選購鑽石的例子說明其運作原理。
故事是這樣的:我的奶奶曾經留給我一只戒指。這個戒指上有個 1.35 克拉大小的鑲台(setting),可惜上面沒有安任何鑽石。某天,我萌生了修復這只戒指的念頭,所以我找了一間珠寶行詢價,以了解我需要準備多少錢。
到了珠寶行以後,我發現店裡既沒有 1.35 克拉的鑽石,也沒有價格。但我沒有因此打退堂鼓。我拿起了紙跟筆,把店裡所有其他鑽石的尺寸跟價格都抄了下來。

我發現絕大部分的鑽石都在 2 克拉以下,所以我畫了一條橫軸以紀錄鑽石的重量。
接下來我畫了一條用來記錄價格的縱軸。
於是上圖就有了座標系的兩軸。在一座像曼哈頓有著網格道路系統(gridded streets)的城市裡,讀者可以循著南北向、東西向道路找出任何交叉路口;同理,在一個座標系裡,讀者可以利用橫軸和縱軸上的位置鎖定任何點。所以我們可以先根據鑽石的重量,從紀錄克拉數的橫軸往上畫一條直線,再根據鑽石的價格,從紀錄價格的縱軸往右畫另一條直線。兩條直線的交點,就是第一個鑽石的資料。
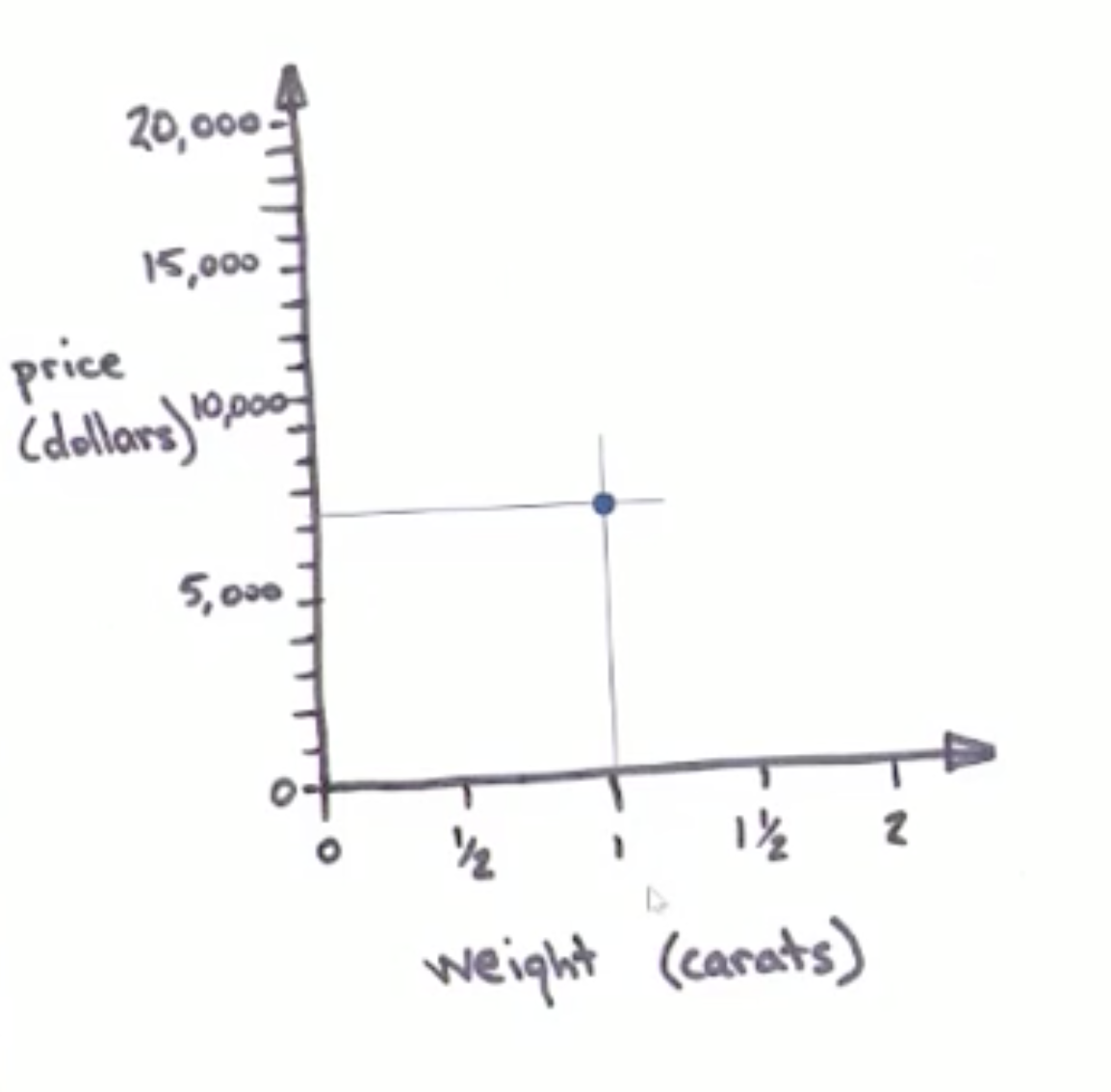
用同樣的方法,我們可以把所有鑽石畫在這個座標系上。
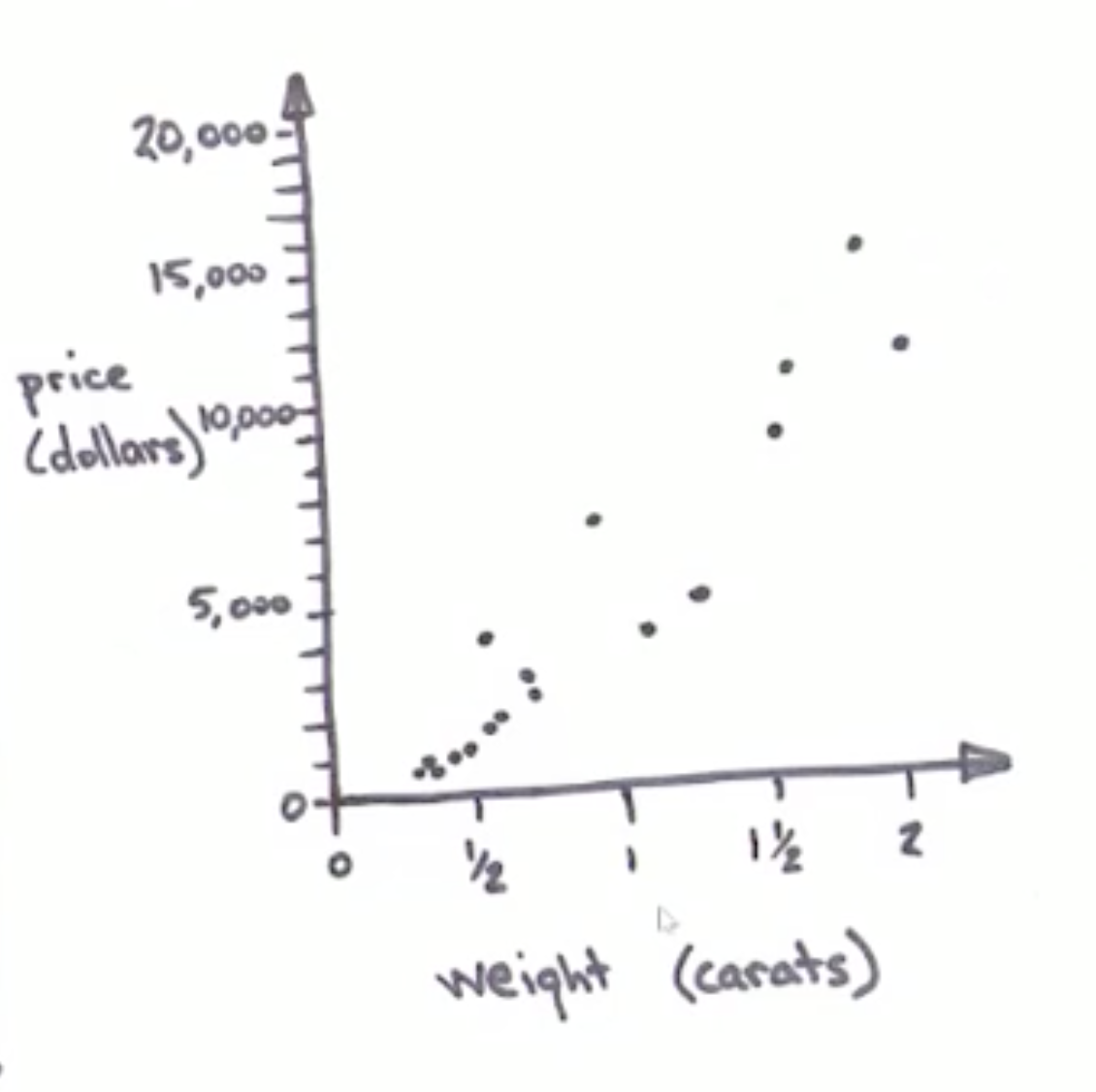
於是一開始的表格變成了一張散點圖。到目前為止,我沒有增加或捨棄任何資訊,我只是換了另一種表達方式,也就是散點圖。從圖片裡我們可以看出一個明顯的形狀,好像有條很寬的直線往右上方延伸。所以我的下一步是在這個範圍內將這條直線畫出來。當這條直線穿過資料時,在它的上下兩側會分佈著差不多數量的資料點。
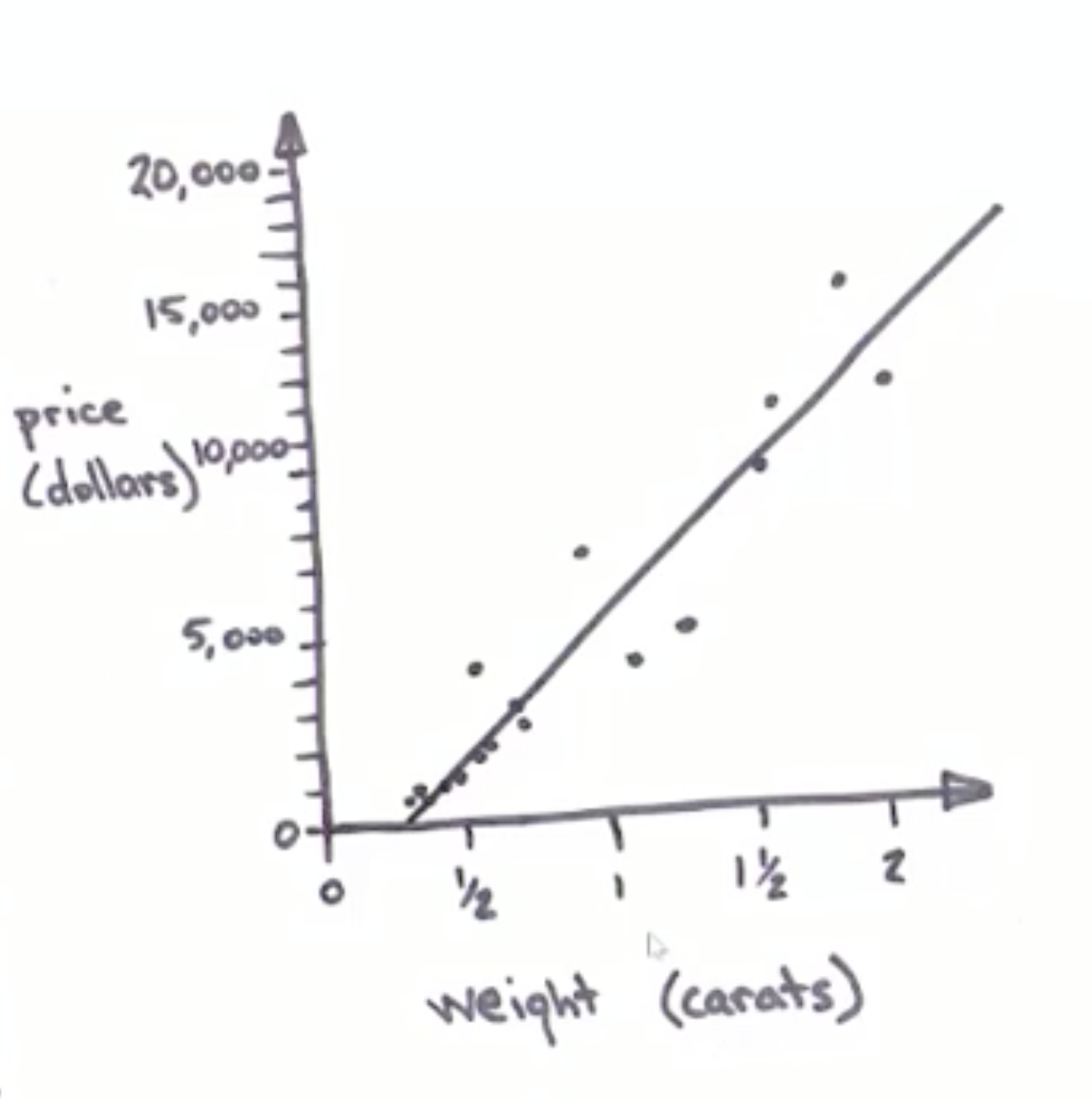
將這條直線畫出來是很關鍵的一步。雖然這條線在我們看來很明顯,但這是因為我們早就具備了媲美超級電腦、擅長辨認特徵的神經運算能力。在畫這條線的時候,我們將原本的資料提煉成了更簡單的形式,就像將真實的影像化約為簡單的漫畫(線條)。雖然在這一步,我確實捨棄了一些資訊,但我也能利用這個簡化模型回答前面的問題。找出符合資料規律的直線,就叫線性迴歸(譯註一)。
有了線性模型以後,我終於可以回答前面的問題:「1.35 克拉的鑽石多少錢?」要回答這個問題,我只需要用看的,先從橫軸上的 1.35 克拉對到模型上,再從模型對到縱軸上,就能知道價格大約是 8,000 元。問題解決!
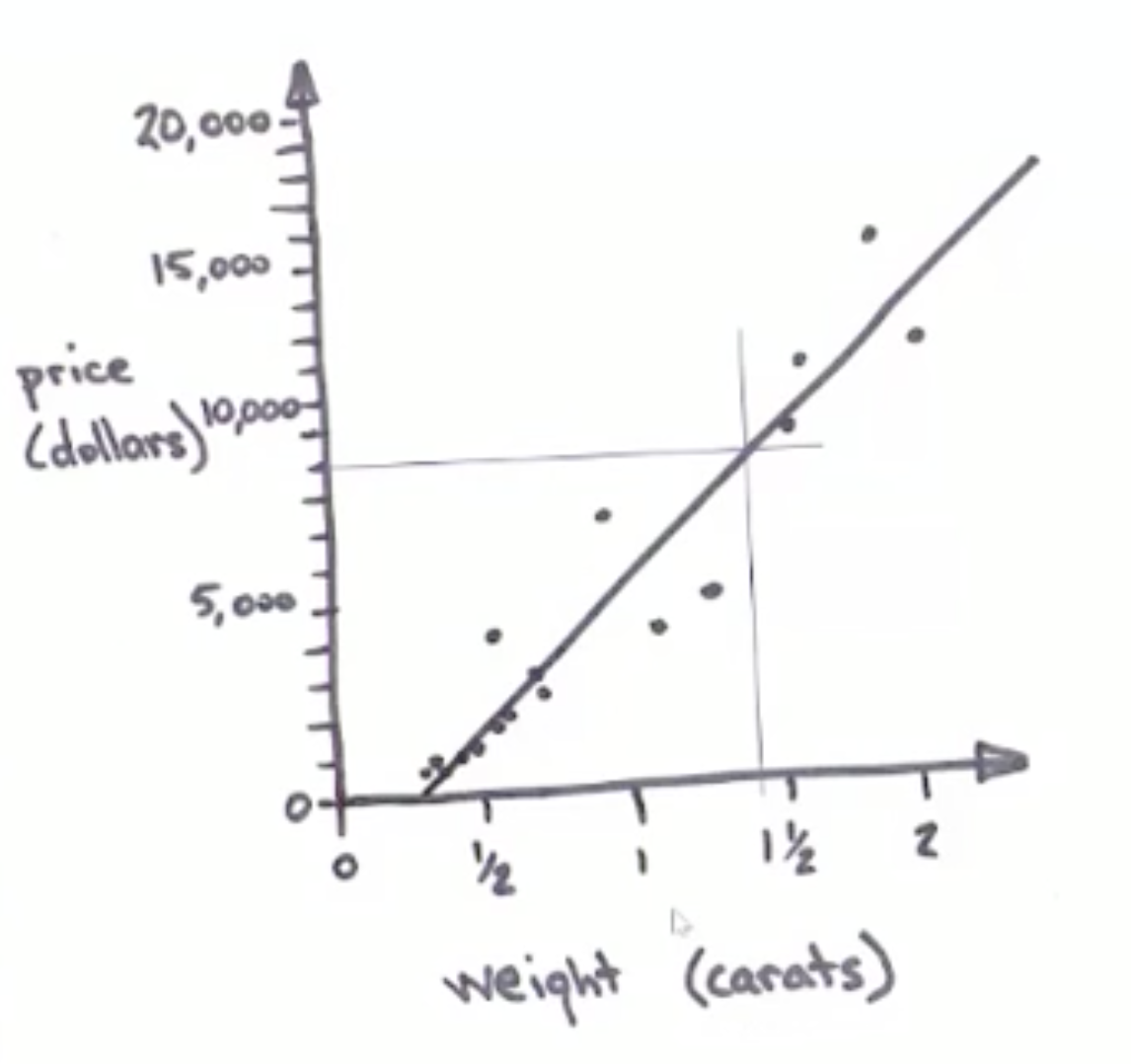
為了讓這個估計值更符合現實情形,我注意到大部分的觀測值並不直接落在模型的線上,這代表我要買的 1.35 克拉鑽石大概也不會剛好是 8,000 元。所以一個很明顯的問題是「實際價格會多接近 8,000 元?」為了瞭解這點,我在直線的兩側畫了涵蓋大部分(差不多 95%)觀測值的範圍。
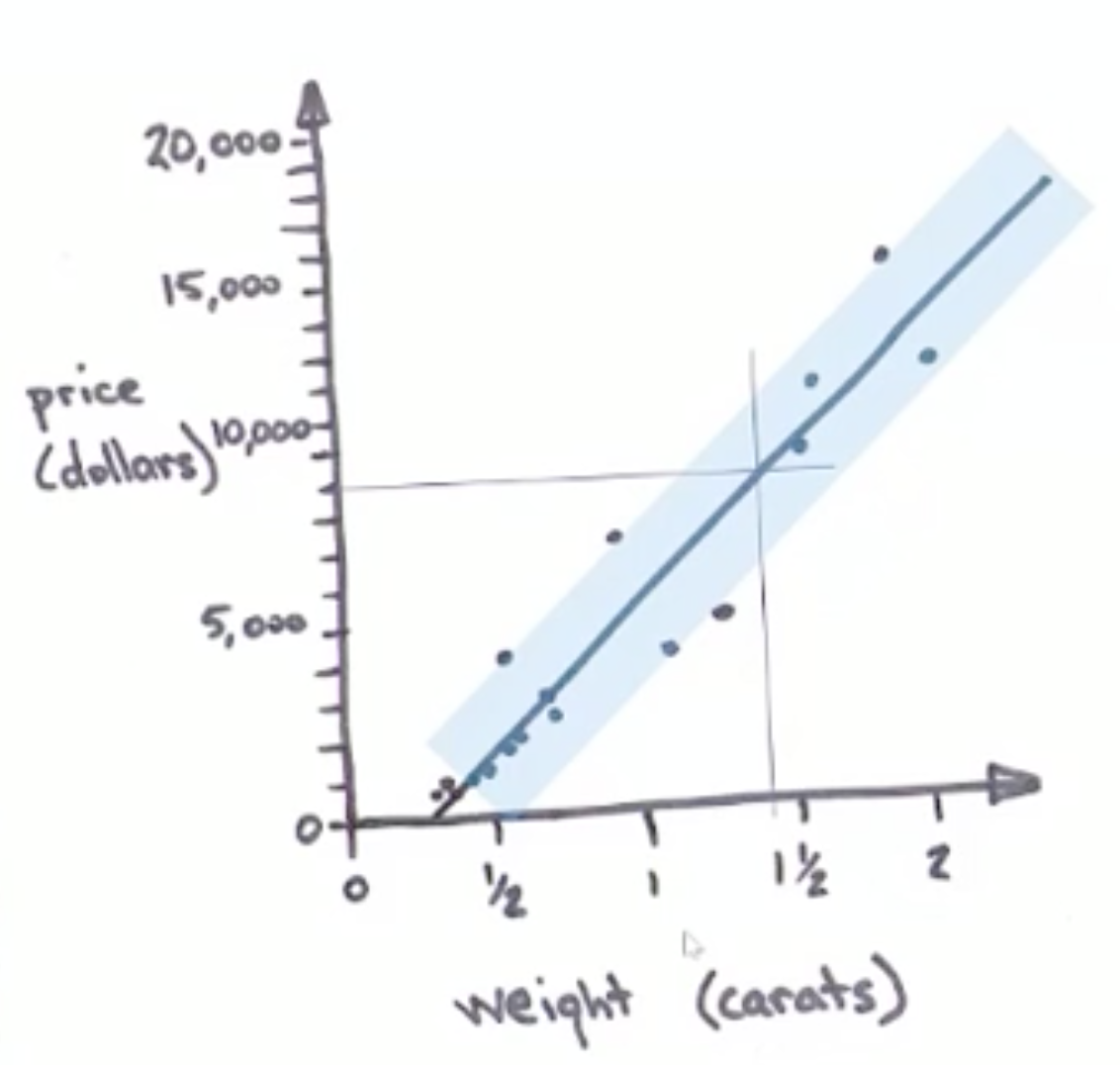
如此一來,我可以說我有(大約 95% 的)信心認為未來任何鑽石的價格和重量都會落在這個範圍內。為了瞭解這和我要找的鑽石有什麼關係,我又沿著 1.35 克拉的垂直線,從價格範圍的上下兩端多看了兩條水平線。
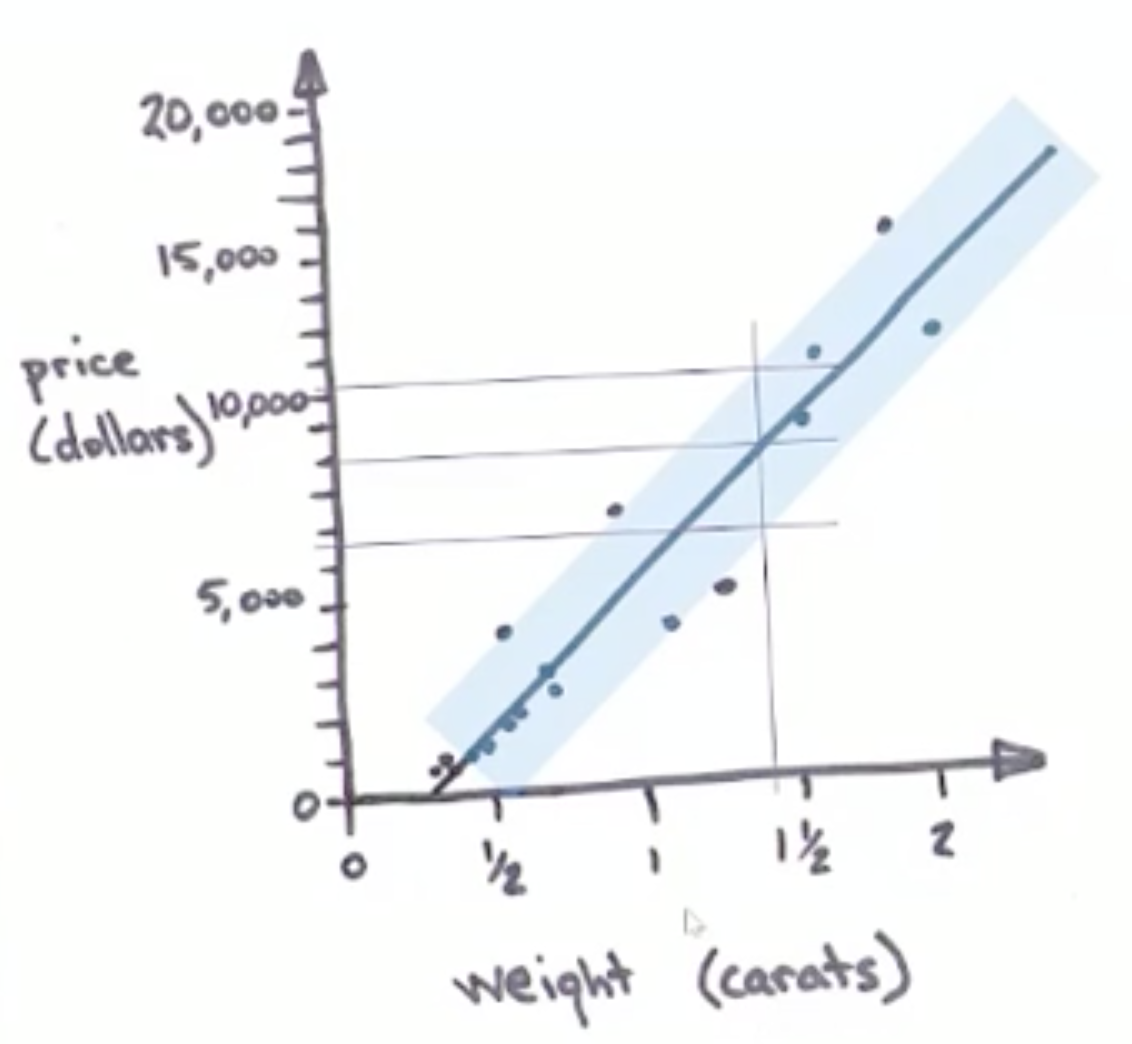
現在我滿有自信地說:「我要找的鑽石,價格不會低於 5,800,但也不會超出 10,200。」了解了這點以後,我就可以開始規劃要花多久,定期從薪水中存入一筆「奶奶的鑽戒修復基金」。
藉著這個例子,我希望說明線性迴歸至少在觀念上是個很簡單的方法。任何人都可以用一支筆、一張餐巾紙和雙眼完成線性迴歸分析,而不一定要使用電腦或數學知識。不過實務上具備數學知識還是很有用的。
在鑽石的例子裡,如果我搜集更多資訊,例如顏色、淨度、切割和內含物數量,此時資料的維度會從原本的兩個增加為六個,也就更難化為圖形。這時數學知識就能幫助我們在六個維度中「畫出」一條直線(譯註二)。
另一方面,如果上面的資料不只有 17 筆,而是 1,700 甚至 1,700 萬筆,就算是最厲害的藝術家也很難從中畫出直線,這時電腦就派上用場了。
Brandon,於 2016 年 12 月 20 日
譯註
「找出符合資料規律的直線,就叫線性迴歸」的原文為 Finding the curve that best fits your data is called regression, and when that curve is a straight line, it's called linear regression. 雖然我以前學的說法是「只要因變量為自變量的線性組合,就可以稱作線性迴歸」,這代表就算線條不是直的,也可能是線性迴歸;但如果將包括多項式的迴歸細分作 polynomial regression,將作者說法算作 simple linear regression 也沒錯。
這邊的數學知識應該以線性代數(linear algebra)為主,所使用的工具為矩陣(matrix)運算。