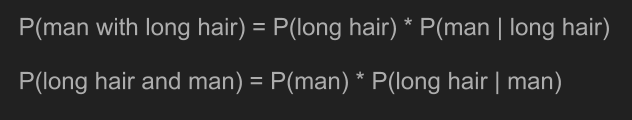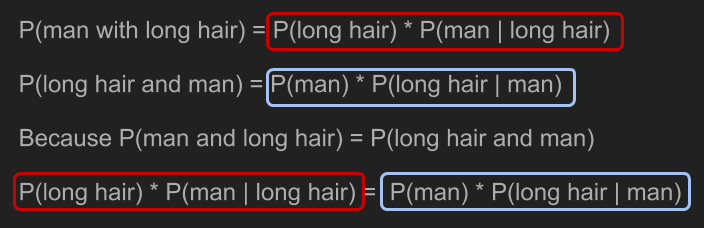貝葉斯推斷的運作原理

原文：How Bayesian inference works

Translated from Brandon Rohrer's Blog by Jimmy Lin

• Google 簡報上的投影片

貝葉斯推斷（Bayesian Inference）是一套可以用來精進預測的方法，在資料不是很多、又想盡量發揮預測能力時特別有用。

雖然有些人會抱著敬畏的心情看待貝葉斯推斷，但它其實一點也不神奇或神秘，而且撇開背後的數學運算，理解其原理完全沒有問題。簡單來說，貝葉斯推斷可以幫助你根據資料，整合相關資訊，並下更強的結論。

「貝葉斯推斷」取名自一位大約三百年前的倫敦長老會（Presbyterian）牧師——湯瑪士．貝葉斯（Thomas Bayes）。他寫過兩本書，一本和神學有關，另一本和統計學有關，其中包含了當今有名的貝氏定理（Bayes Theorem）的雛形。這個定理之後被廣泛應用於推斷問題，即用來做出有根據的推測。如今，貝葉斯的諸多想法之所以會這麼熱門，另一位主教理查德·普莱斯（Richard Price）也功不可沒。他發現了這些想法的重要性，並改進和發表了它們。考慮到這些歷史因素，更精確一點地說，貝氏定理應該被稱作「貝葉斯－普萊斯規則」。

電影院裡的貝葉斯推斷

請讀者先想像你人在電影院，剛好看到前面有個人掉了電影票。這個人的背影如上圖所示，你想叫住他／她，但你只知道這個人有一頭飄逸長髮，卻不知道他／她的性別。問題來了：你該大喊「先生，不好意思」還是「女士，不好意思」？根據讀者對兩性頭髮長度的印象，你或許會認為這個人是女的。（在這個簡單的例子裡，我們只考慮長髮和短髮、男性和女性。）

但現在考慮另一個狀況：如果這個人排在男性洗手間的隊伍當中呢？多了這項資訊，讀者或許會認為這個人是男的。我們可以不經思索地根據不同的常識和知識調整判斷，而貝葉斯推斷正是將這點化為數學，幫助我們做出更精準的評估。

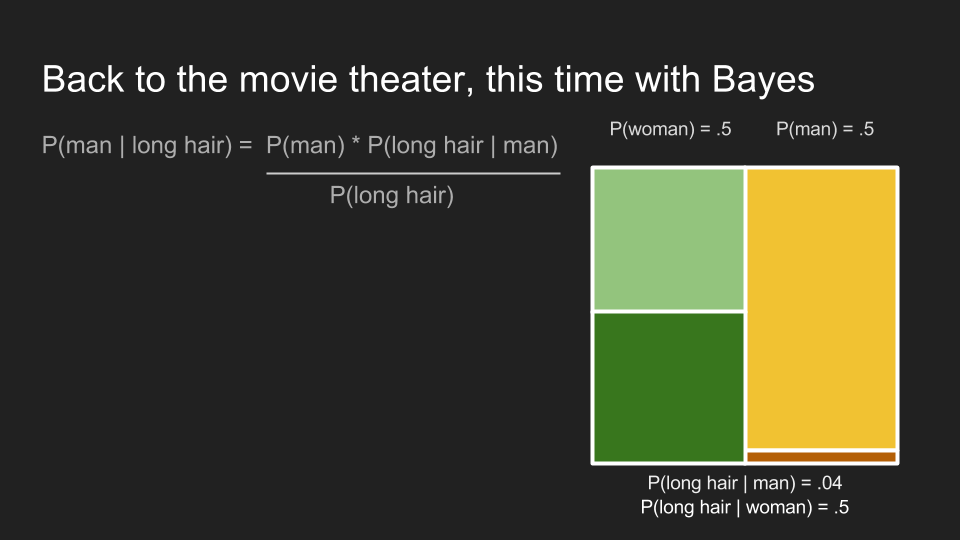
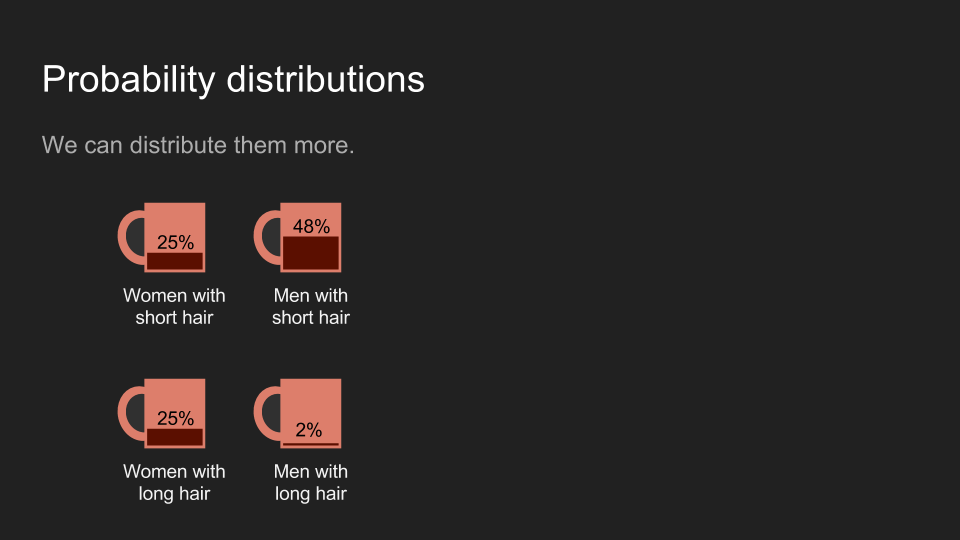
為了將前面的例子用數學表達，我們可以先假設電影院裡的人有一半是女的，有一半是男的。也就是說 100 個人裡面，有 50 名男性和 50 名女性。在這 50 名女性裡，有一半的人有長髮（25 人），另一半有短髮（25 人）；在 50 名男性當中，48 個人有短髮，兩個人有長髮。因為在 27 位長髮觀眾裡，有 25 位是女性和兩位男性，所以前面第一個猜測很安全。

但如果我們換一個場景：在男性洗手間隊伍的 100 個人裡面，有 98 位男性和兩位陪伴中的女性。這裡的女性雖然也有一半是長髮、一半是短髮，但人數減為一位長髮女性和一位短髮女性。男性觀眾中長髮和短髮的比例也不變，不過因為總人數變成了 98 人，現在隊伍裡有 94 位短髮男性，和四位長髮男性。由於現在長髮觀眾中有一名女性和四名男性，保守的猜測變成了男性。從這個例子，我們可以很容易地理解貝葉斯推斷的原理。根據不同的先決條件——也就是這名觀眾是否站在男性洗手間的隊伍裡，我們可以做出更準確的評估。

為了好好說明貝葉斯推斷，我們最好先花點時間清楚定義一些觀念。很不湊巧這段會用到一些數學，不過我們會避免談任何不必要的細節，請讀者務必耐心讀完以下幾段，這對理解之後的內容很有幫助。為了打好基礎，我們需要快速認識四個觀念：機率（probabilities）、條件機率（conditional probabilities）、聯合機率（joint probabilities）和邊際機率（marginal probabilities）。

機率

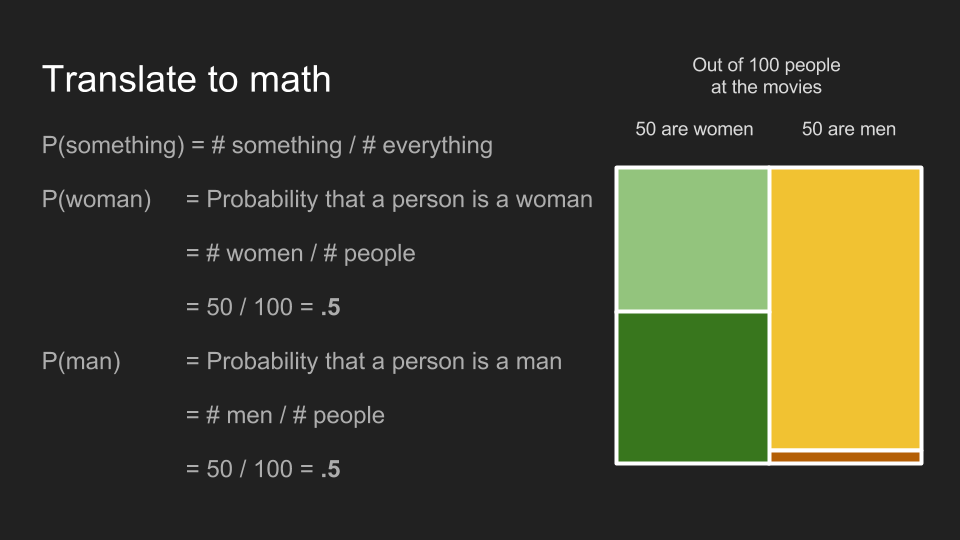
某事件發生的機率，就是將「該事件的數量」除以「所有可能發生的事件數量」。在我們的例子裡，某位觀眾是女性的機率是 50 名女性除以 100 位觀眾，即 0.5 或 50%。觀眾是男性的機率也是 50%。

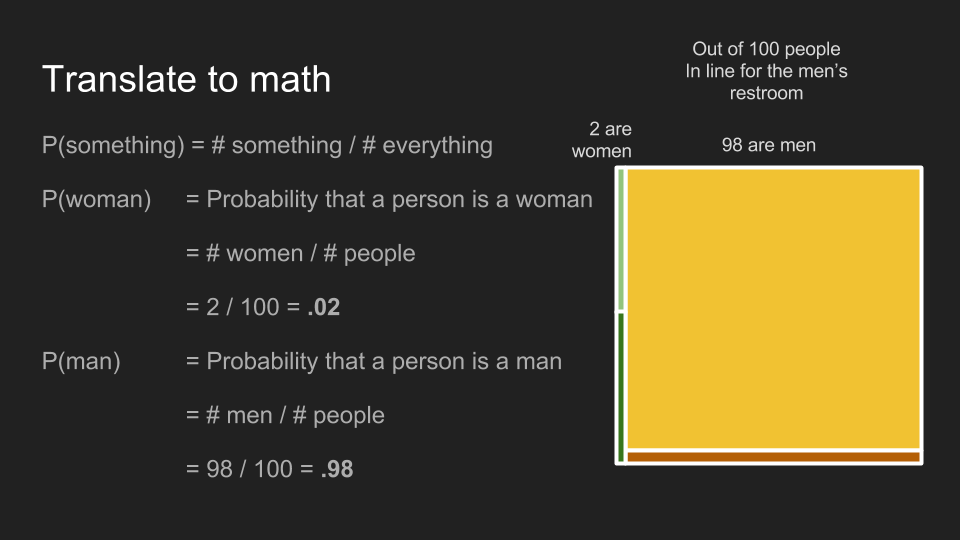
在男性洗手間的隊伍裡，觀眾是女性的機率為 0.02，男性的機率為 0.98。

條件機率

條件機率所能回答的問題是「如果這名觀眾是女性，那她有長頭髮的機率為何？」條件機率的計算方式和一般機率相同，只不過條件機率只會涉及符合條件的少部分樣本。在我們的例子裡，女性觀眾中有長髮的條件機率 $P(long \space hair | woman)$ 即「長髮女性人數」除以「女性總人數」，也就是 0.5。不管我們是計算電影院裡的觀眾，還是男性廁所隊伍裡的觀眾，都會得到相同的條件機率。

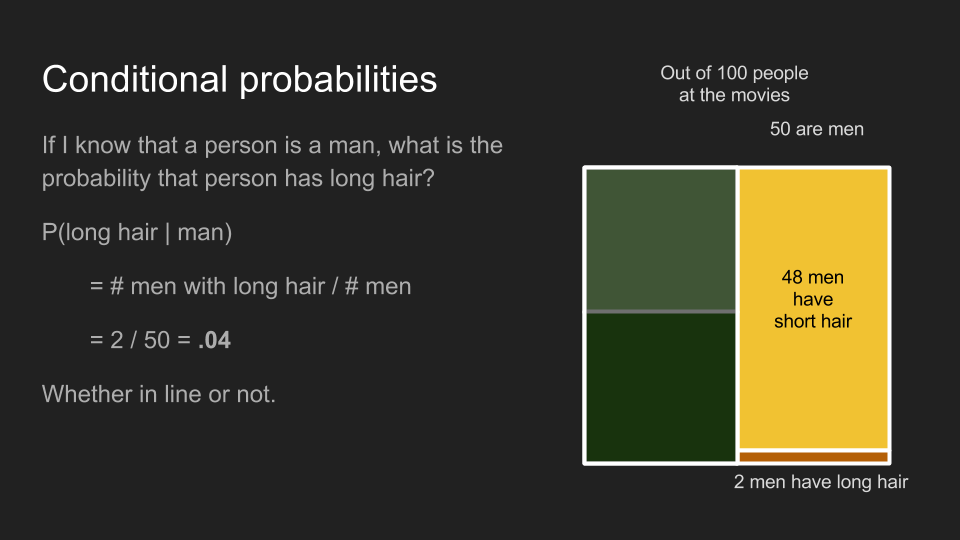
運用相同的方法，男性觀眾中有有長髮的條件機率 $P(long \space hair | man)$ 為 0.04，不管是隊伍裡還是隊伍外的男性。

關於條件機率，有一件需要特別注意的事：$P(A | B)$ 並不等於 $P(B | A)$。例如 $P (cute | puppy)$ 並不等於 $P (puppy | cute)$。如果我手上抱著的東西是一隻狗狗，那這個東西很可愛的機率就很高，但如果我只知道我手上抱著的東西很可愛，那這個東西是狗狗的機率只有中下，因為它也有可能是貓貓、兔兔、小刺蝟或小嬰兒。

聯合機率

聯合機率適合用來回答這類問題：「這位觀眾是一名短髮女性的機率為何？」回答這個問題的過程分為兩個步驟。首先，我們會先找出觀眾是女性的機率 $P(woman)$；接著，我們再找出在女性觀眾中短髮的條件機率 $P(short \space hair | woman)$。將兩個機率相乘，就可以得到前面問題所求的聯合機率，即 $P(woman \space with \space short \space hair) = P(woman) * P(short \space hair | woman)$。利用這個方法，我們可以重算一次之前的結論——電影院裡，某位觀眾為長髮女性的機率 $P(woman \space with \space long \space hair)$ 為 0.25，但男性洗手間的隊伍裡，某位觀眾為長髮女性的機率 $P(woman \space with \space long \space hair)$ 為 0.01。兩者之所以不同，是因為觀眾為女性的機率 $P(woman)$ 在兩個情況下不同。

同理，我們也可以算出電影院裡，某位觀眾為長髮男性的聯合機率 $P(man \space with \space long \space hair)$ 為 0.02，但在男性洗手間隊伍裡的聯合機率則為 0.04。

聯合機率和條件機率不同的地方，在於聯合機率的計算順序並不影響結果。也就是說 $P(A \space and \space B)$ 和 $P(B \space and \space A)$ 是一樣的。我喝牛奶又吃果醬甜甜圈（jelly donut）的機率，和我吃果醬甜甜圈又喝牛奶的機率是一樣的。

邊際機率

最後，我們需要了解的是邊際機率，它可以用來回答這類問題：「某位觀眾有長髮的機率為何？」要回答這個問題，我們需要將所有符合這個條件的事件發生機率加總——即長髮男性和長髮女性的聯合機率。將這兩個聯合機率相加以後，我們可以得出在電影院裡的觀眾是長頭髮的機率 $P(long \space hair)$ 為 0.27，但在男性洗手間的隊伍裡這個機率只有 0.05。

貝氏定理

介紹完四個重要的觀念以後，終於可以來談我們關心的問題了。我們想要了解「如果我們知道某人有長頭髮，這個人是女性（或男性）的機率為何？」這也是條件機率 $P(man | long \space hair)$ 的解，但我們現在只知道順序相反的情況 $P(long \space hair | man)$，即「如果我們知道某人是男性，這個人有長頭髮的機率為何？」因為條件機率的順序不可任意調換，我們還沒辦法回答這個問題。

幸好湯瑪士．貝葉斯早就發現了一個可以為我們解答的神奇工具。

根據聯合機率的計算方法，我們可以將前面兩個條件機率寫成「男性且長髮」$P(man \space with \space long \space hair)$ 和「長髮且男性」$P(long \space hair \space and \space man)$ 的計算式。由於聯合機率的順序是可以互換的，兩者完全相同。

利用一點代數計算，我們就能解決前面的問題，即求出 $P(man | long \space hair)$。

將「長髮」和「男性」以 A 和 B 代換，我們就得到了貝氏定理。

最後我們終於可以解決前面的電影票問題了。這裡我們可以應用貝氏定理。

首先，我們需要求出長髮觀眾的邊際機率，$P(long \space hair)$。

接下來，我們可以代入前面的數字，並算出長髮觀眾為男性的機率。在男性洗手間的隊伍裡，該機率 $P(man | long \space hair)$ 為 0.8。這印證了我們先前認為長髮觀眾應該為男性的直覺。也就是說，貝氏定理印證了我們在該情況下的直覺。更重要的是它融合了我們對男性隊伍中，男性人數遠大於女性的既有資訊。利用這項資訊，貝氏定理更新了我們在該狀況下的信念（belief）。

機率分佈

雖然電影院這類的例子，已經足以說明貝葉斯推斷的重要性和運作原理，但在資料科學的應用中，貝葉斯推斷最重要的功用是用來解釋資料。在擁有少量資料的情況下，我們可以藉著融入問題的背景知識以做出更強的結論。這點我會再詳細說明，但請先容許我再多介紹一個概念——我們需要先弄清楚機率分佈（probability distributions）到底是什麼。

讀者可以先將機率想成一壺剛好可以倒滿一個杯子的咖啡。如果我們只有一個杯子，那就沒什麼需要討論的問題了；但如果我們有很多杯子，我們就需要決定要給每個杯子倒多少咖啡。讀者可以任意決定咖啡的量，只要將咖啡倒完就好。在剛才的電影院問題裡，我們可以將男性和女性比喻為杯子。

我們也可以用四個杯子比喻兩個性別和兩種頭髮長度的組合。不管比喻為何，全部咖啡加總都應該是一個杯子的量。

一般來說，我們會將這些杯子排成一排，這時咖啡的量可以看作是一張直方圖（histogram）。我們可以將咖啡想成我們的信念（belief），並將咖啡在不同杯子裡的分佈，想成對不同的結果的信念強烈程度。

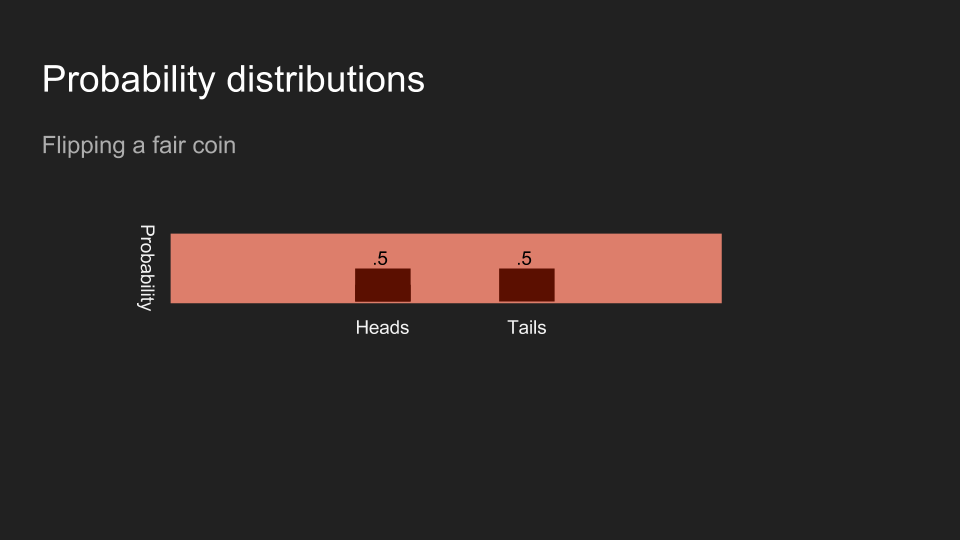
如果我擲一枚硬幣，而且不讓讀者看到結果，讀者對硬幣正反面的信念應該是一半一半。

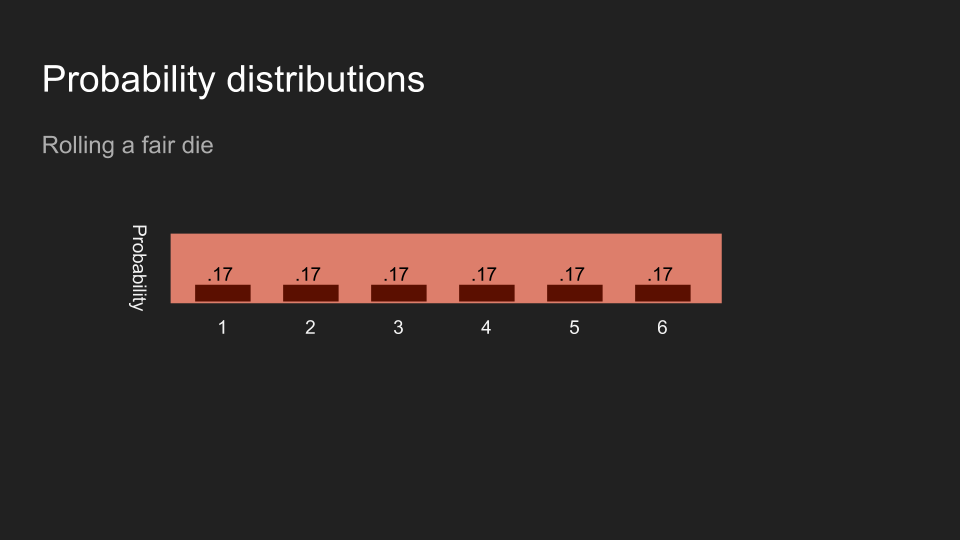
如果我丟一個骰子，而且不讓讀者看到結果，讀者對骰子正面數字的信念應該會平均分佈於六個數字。

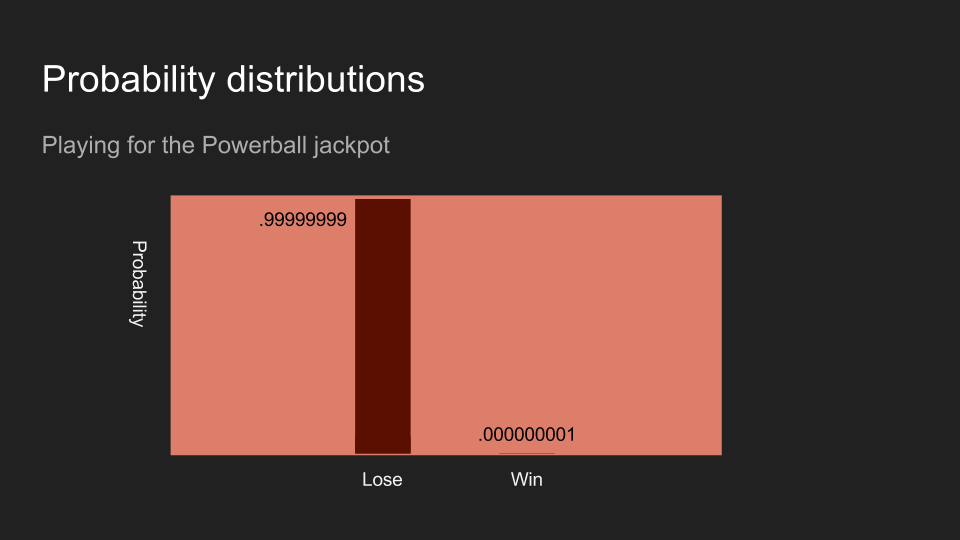
如果我買了一張彩券，讀者對贏得彩券的信念應該會趨近於零。以上三個例子：擲硬幣、丟骰子、和買彩券，都是資料測量和收集的例子。

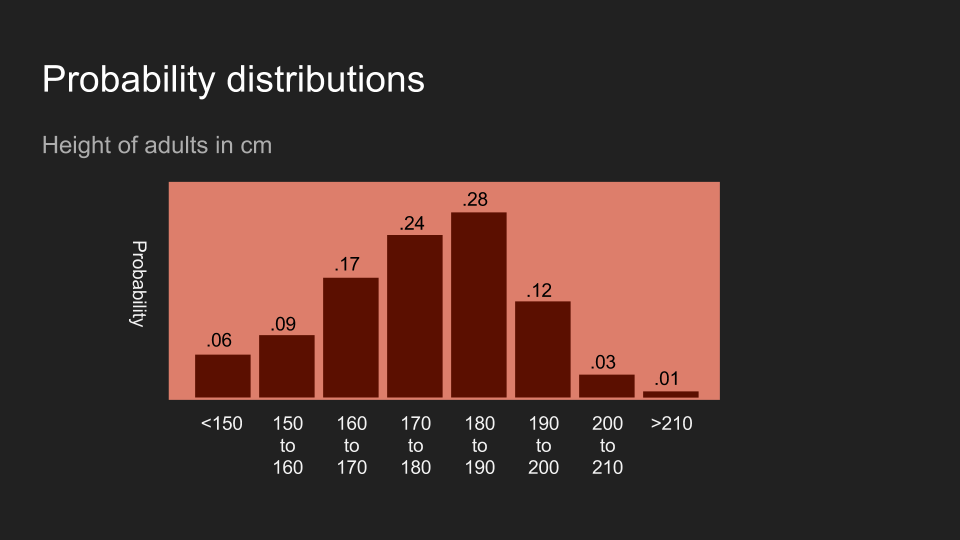
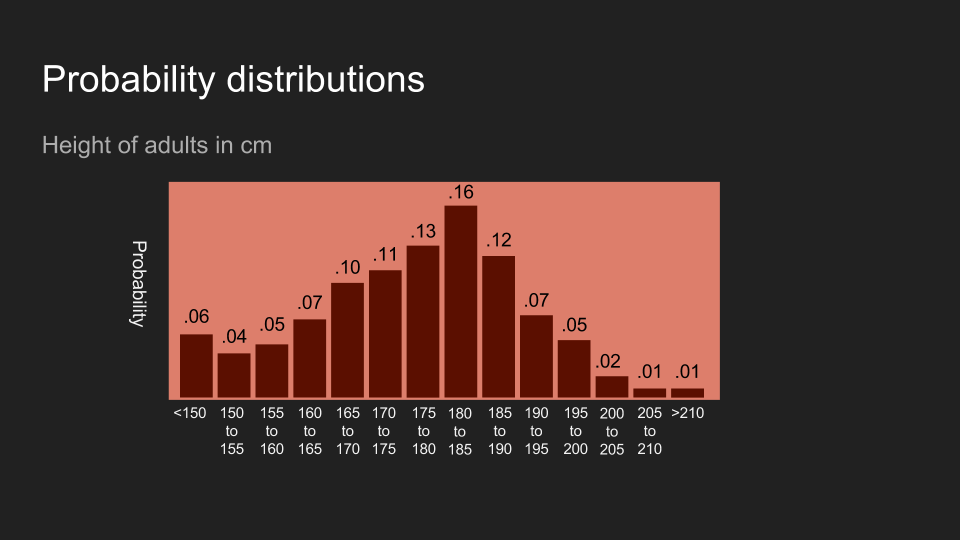
不意外地，讀者也可以對其它形式的資料抱持著一定的信念。以美國成人的身高為例，如果我說我剛量完某人的身高，讀者的信念可能會和上面的圖片類似。這代表讀者相信這個人的身高應該介於 150 到 200 公分，而且最有可能介於 180 和 190 公分。

我們還可以將分佈中的群類（bin）分得更細。讀者可以把這想成將咖啡分到更多杯子中，每個杯子分的咖啡更少，信念的分佈也更細緻。

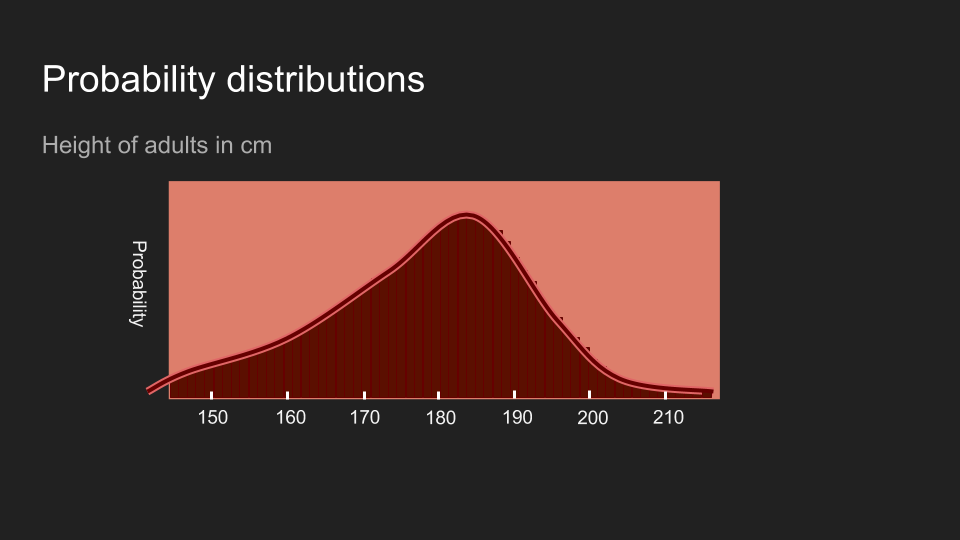
等杯子數量多到一個程度以後，我們就不太能用杯子來比喻了。在這個情況下，機率的分布變得連續，需要不同的計算方法，但是背後的概念還是很管用：機率分佈反映了信念的分佈。

感謝讀者的耐心。在介紹完了機率分佈以後，我們可以利用貝葉斯推斷來解讀資料了。為了說明整個流程，我們來量一下我的狗狗的體重。

獸醫院裡的貝葉斯推斷

我的狗狗名叫阿怖（Reign of Terror）。當我帶她去看獸醫時，她會在體重計上扭來扭去，這讓量體重變成一件很困難的事。但是了解精確的體重很重要，因為如果她變重了，我們就得減少阿怖的食物量。由於阿怖把食物看得比自己的命還重，量好體重真的很重要。

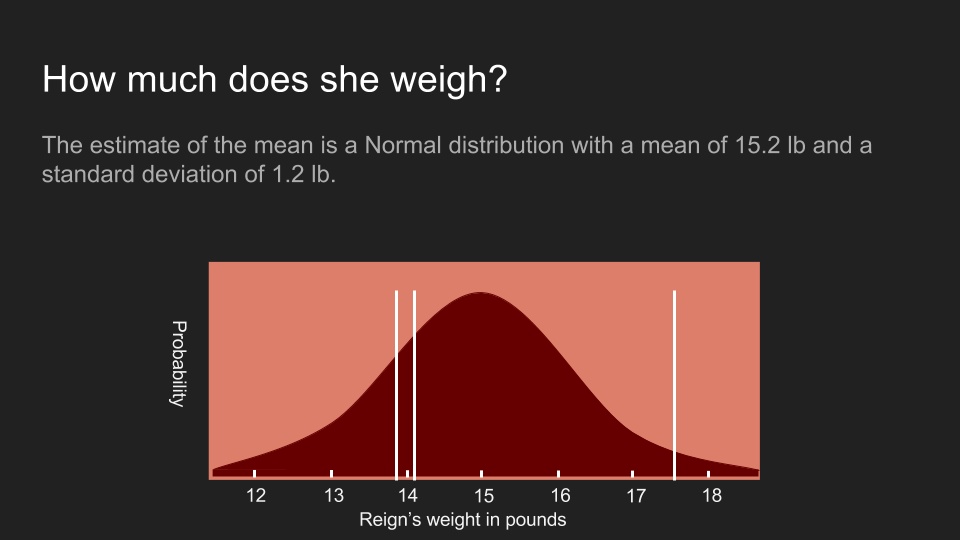
我們上次去看獸醫的時候，在阿怖變得無理取鬧之前獸醫量到了三個體重：13.9 磅、17.5 磅和 14.1 磅（翻註：一磅約等於 0.45 公斤）。我們可以按一套標準的統計方法，將這些數據化為機率分佈。我們可以先計算這組數據的平均值、標準差（standard deviation）和標準誤差（standard error），再建立一套阿怖的體重分佈。

根據這個方法所得出的分佈，顯示了我們對阿怖體重的信念。阿怖的體重呈常態分佈（normal distributed），有著 15.2 磅的平均值，以及 1.2 磅的標準誤差。圖上的白線是我們實際測量到的三個數值。不過很不湊巧地，這個分佈曲線有點太寬了。雖然最大值位於 15.2 磅，但這個機率分佈顯示阿怖的體重還是很有可能低於 13 磅或超出 17 磅。在這麼寬的範圍裡，我們很難做出任何確切的決定。通常我們遇到這種情況時，會選擇回去收集更多資料，但有時這麼做不太可行或成本很高。在我們的例子裡，阿怖已經失去了耐心，所以我們只能利用這三組數值。

這時貝氏定理就派上用場了。貝氏定理很適合用來充分利用少量資料。在實際應用之前，我們可以先來回顧一下貝氏定理的算式和每個部分。

我們先將算式中的 A 和 B 換成體重（w，weight）和測量結果（m，measurement），以便說明如何使用貝氏定理。圖片中的四個部分分別代表不同的處理步驟。

首先，事前機率（prior probability）$P(w)$ 代表我們的事前信念。在這個例子裡，事前機率就是我們在將阿怖放上體重計前，對她體重分佈的信念。

算式中的概似機率（likelihood）$P(m | w)$ 代表在某個既定體重下，我們得到這些測量結果的機率。這也被稱作資料的概似機率（the likelihood of the data）。

事後機率（posterior probability）$P(w | m)$ 則代表在某測量值出現的情況下，阿佈實際體重為 $w$ 的機率。這也是我們最關心的部分。

最後，資料機率（probability of data）$P(m)$ 代表我們得到某測量值的機率。在這個例子裡，我們就假設這是一個常數，即體重計本身沒有誤差。

我們可以先放心拋開所有假設，當作自己完全不知道任何狀況。也就是說在這個例子裡，我們可以假設阿怖的體重為 13 磅、15 磅、一磅甚至一百萬磅的機率完全相等，讓資料說話。為了做到這點，我們假設事前機率為均勻分佈（uniform distribution），即任何體重發生的機率都是一個固定的常數。這可以幫助我們將貝氏定理簡化為 $P(w | m) = P(m | w)$。

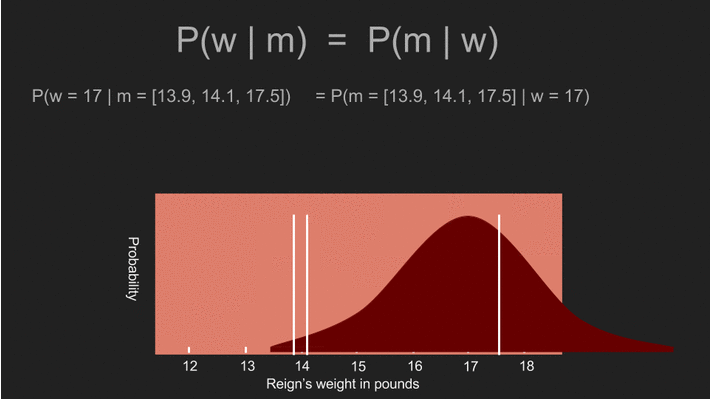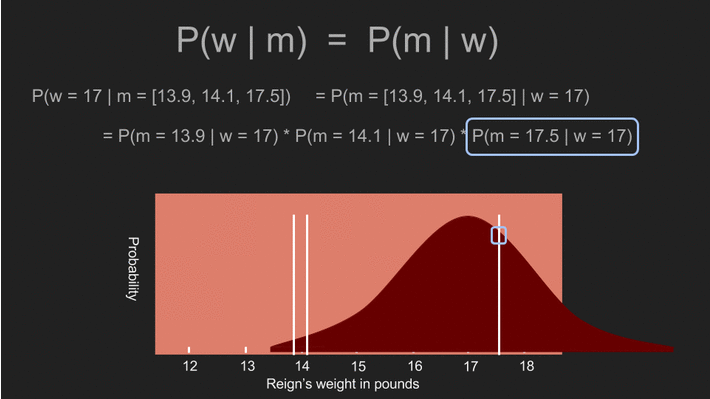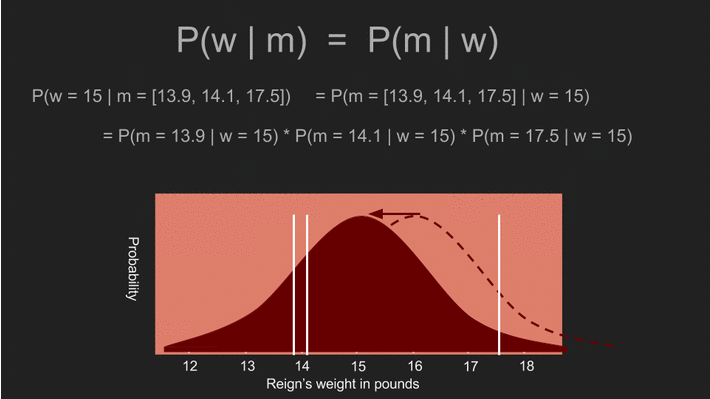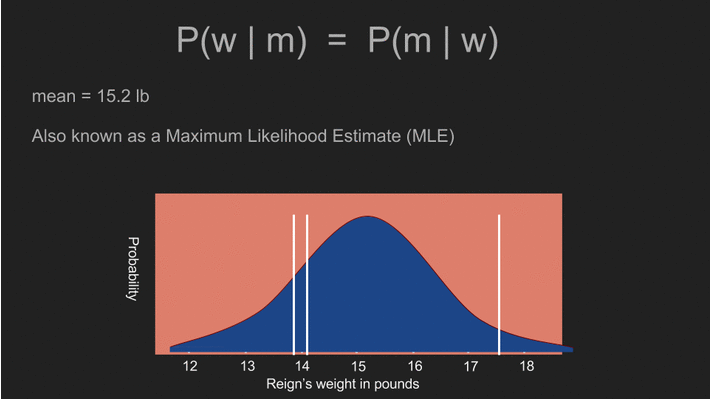
現在我們用阿怖所有可能的體重來計算得到這三組測量值的概似機率。例如，如果阿怖的體重是一千磅，那我們得到這三組測量值的機率應該是微乎其微。但如果阿怖的體重介於 14 到 16 磅之間，這三組測量值出現的機率就很高。我們可以利用不同的體重，重複計算得到特定測量值的機率，即 $P(m | w)$。由於我們假設事前機率為均勻分布，這也是事後機率 $P(w | m)$ 的估計值。

這麼做所得到的答案，會和前面利用平均值、標準差和標準誤差所算出的答案非常相似。實際上，兩個答案確實完全一模一樣，因為利用均勻分佈的事前機率，就會得到傳統統計方法下的估計值。機率分佈曲線中的最高點，即平均值 15.2 磅，也被稱為阿怖體重的最大似然估計值（maximum likelihood estimate，MLE）。

雖然我們利用了貝氏定理，但我們還沒得到真正有用的估計值。為了達成這個目的，我們需要一個非均勻分布的事前機率。事前機率代表在測量前我們對某件事物的信念，而一個均勻分布的事前機率，則代表我們認為任何結果發生的機率都一樣。但這種情況其實不常見，因為我們通常對於測量的事物本身都有一定的認識。比方說，年齡永遠只會大於零、氣溫永遠比攝氏 -276 度還高、成人的身高很少超過八英尺（約 244 公分）。我們通常能運用一些相關的領域知識（domain knowledge）得知哪些情況發生的機率比較高。

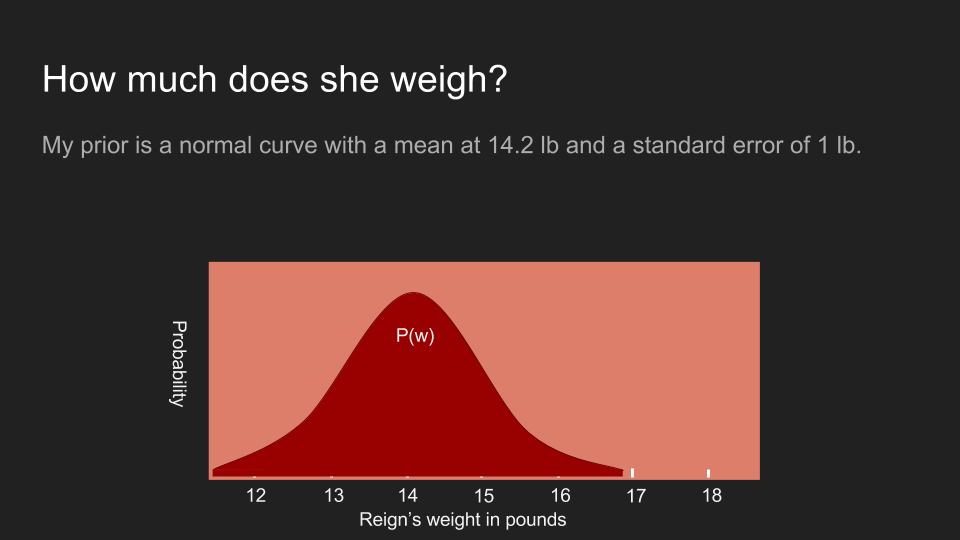
所以在阿怖的例子裡，我確實有一些相關資訊。我知道上次我們來看獸醫的時候，阿怖的體重是 14.2 磅。而且我最近並沒有感覺阿怖變得特別重或輕，儘管我的手臂不如體重計靈敏。因此，我相信阿怖的體重應該在 14.2 磅附近，有可能變輕或變重一兩磅。為了呈現這個信念，我建構了一個平均為 14.2 磅、標準差為 0.5 磅的正態分佈。

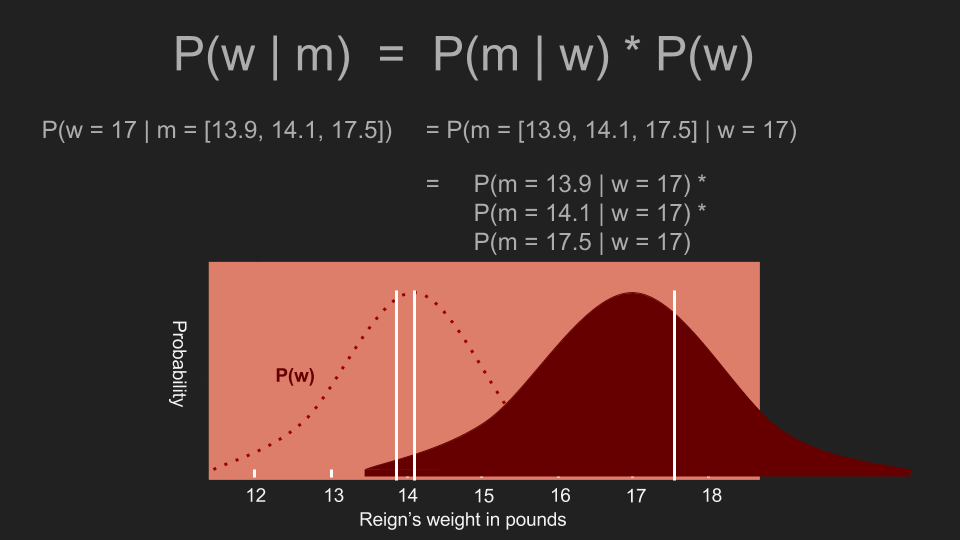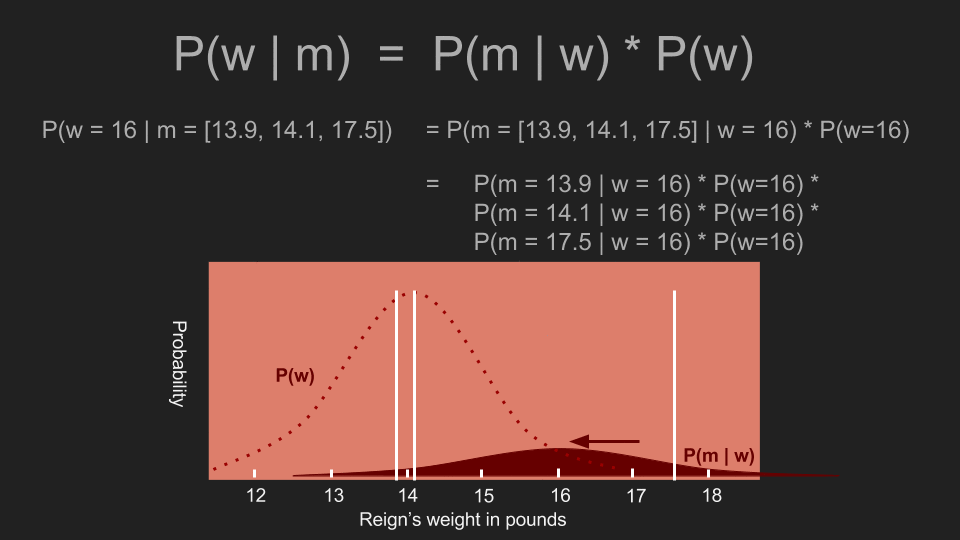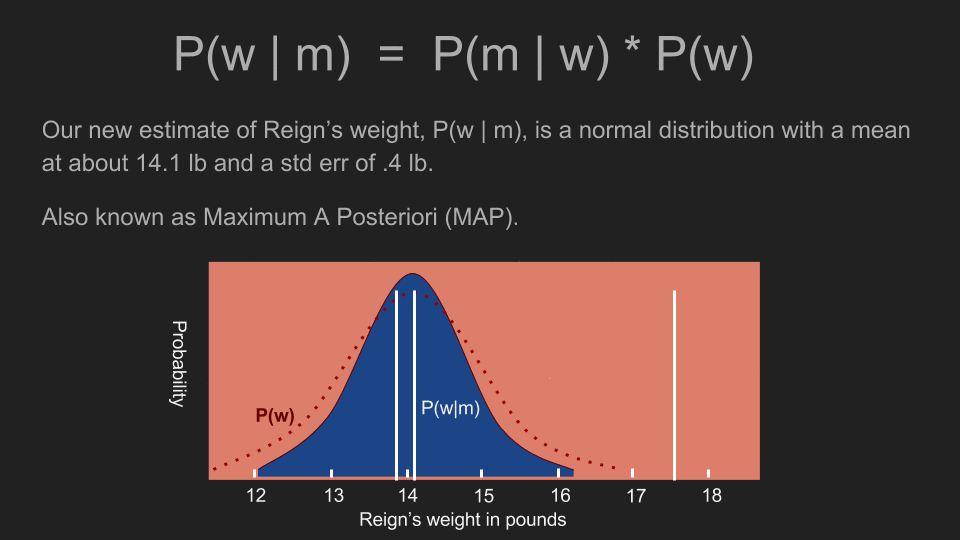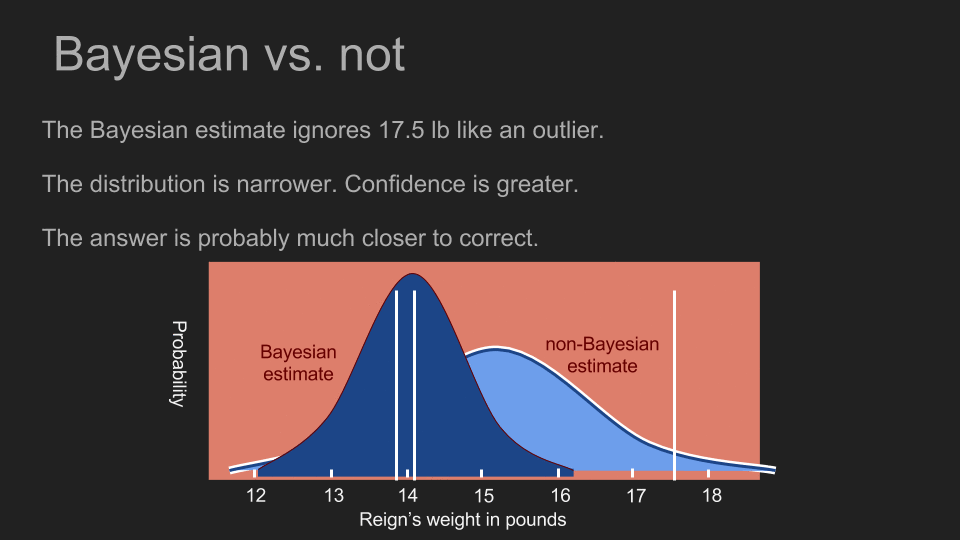
有了這個事前機率後，我們可以重複以上事後機率的計算步驟。為了計算事後機率，我們先計算阿怖體重為一個特定值（例如 17 磅）的機率，再將「（根據事前機率，）阿怖的體重確實是 17 磅的機率」和「在阿怖體重是 17 磅的情況下，得到這些測量值的條件機率」相乘。接著我們可以利用這個方法測試各種可能的體重，這時事前機率所扮演的角色，是壓低或放大某些體重發生的機率。在我們的例子裡，事前機率會為 13 到 15 磅的估計值賦予更多權重，並削弱這個範圍外的權重。這正是採用正態分佈和均勻分布之間的差異。在均勻分布的事前機率下，即使是 17 磅的估計值都還有不錯的發生機率；但在正態分佈的事前機率下，它的發生機率已經處於分佈的尾端了。乘上事前機率會使 17 磅發生的機率變得非常低。

在計算完每個體重的發生機率以後，我們就有了一個新的事後機率分佈。這個分佈曲線的最高點被稱為最大後驗機率（maximum a posteriori estimate，MAP），在這個例子裡為 14.1 磅。這和我們之前利用均勻事前機率所算出的最高點（15.2 磅）差很多。新的高峰也更陡峭，這代表我們可以對這個估計值抱持更高的信心。現在我們可以看出阿怖的體重並沒有什麼變化，她的食物量也不需要增減。

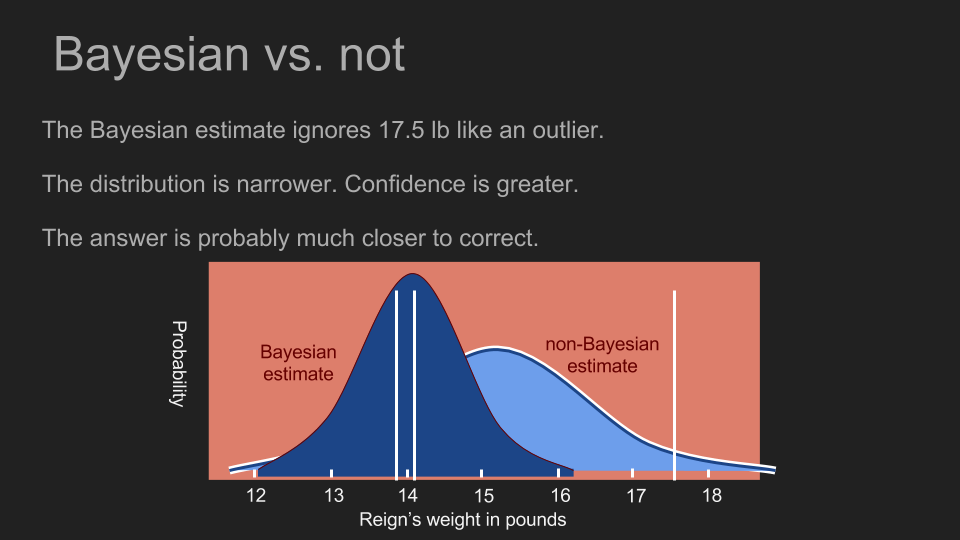
藉由融合我們對測量目標已知的資訊，我們可以做出更精準、更有信心的估計，也能幫助我們善用少量資料。當我們所採取的事前分佈，對 17.5 磅的測量值賦予很低的發生機率時，這幾乎等同於將 17.5 磅當作異常值拒絕。不過我們並不需要憑直覺或知識判斷異常值；貝氏定理可以幫助我們運用數學，解決這個問題。

直得留意的是，在阿怖的例子裡，我們直接假設得到某測量值的機率 $P(m)$ 為均勻分布。但如果我們得知體重計有一定的偏差，也可以將這項資訊融入 $P(m)$ 當中。如果這個體重計只會顯示偶數、有 10% 的機率會顯示 2.0 磅、或是每用三次就會跳出隨機的測量值，我們也可以藉由修改 $P(m)$ 反映這些現象、精進事後機率。

避免貝氏陷阱

雖然在阿怖的例子裡，我們學到了使用貝氏推斷的好處，但同時也該留意潛在的陷阱。我們雖然能藉由對答案作出假設，以提升估計的精確程度，但測量、估計某事物的目的，終究在於更加了解該事物。如果我們認為自己已經知道答案，那這麼做可能反倒是在修正資料。馬克．吐溫（Mark Twain）對此有很精闢的見解：「讓我們陷入困境的不是無知，而是信以為真的謬誤。」

如果我們一開始就武斷地認為阿怖的體重應該介於 13 到 15 磅，那我們可能永遠都不會發現，她的體重其實已經掉到 12.5 磅了。因為不管我們測量多少次，我們所採用的事前分佈都會對 12.5 磅賦予 0% 發生機率，也會忽略所有低於 13 磅的測量值。

幸好有一個方法可以幫助我們規避這個風險：只要至少給每個結果分配一點機率，我們就可以避免盲目地消去任何可能性。如此一來，就算世事難料，阿怖長成了一千磅，我們所得到的測量值也還是能反映在事後機率上。這就是為什麼正態分佈很常被用作事前機率的模型，它一方面可以集中我們對小範圍結果的信念，一方面具有即使無限延伸，機率也永不歸零的長尾。

在這段對話中，紅心皇后就是一個很好的典範：

愛麗絲笑了，說：「試也沒用，一個人不能相信不可能的事。」

「我敢說這是妳練習得不夠，」王后說，「我像妳這樣大的時候，每天練上半小時呢。嘿！有時候，我吃早飯前就能相信六件不可能的事哩！」

——路易斯．卡羅（Lewis Carroll）《愛麗絲夢遊仙境》

修正：感謝發現錯字和錯誤的讀者們！Justin Fortier 和 Irina Max，我欠你們一杯飲料。

Brandon，於 2016 年 11 月 2 日

譯註

1. 《愛麗絲夢遊仙境》節錄的中文翻譯引自黃盛《飛越愛麗絲：邏輯、語言和哲學》。