遞歸神經網路（RNN）和長短期記憶模型（LSTM）的運作原理

原文：How Recurrent Neural Networks and Long Short-Term Memory Work

Translated from Brandon Rohrer's Blog by Jimmy Lin

相關連結：

Google 投影片
本文翻譯自 Elham Khanchebemehr 的英文逐字稿，非常感謝

這幾年，機器學習（machine learning）相關的應用獲得了許多關注，其中有幾大領域特別熱門：其中一個是圖片辨識，像是在網路上搜尋貓咪的圖片，或是將任何問題轉為類似形式；另一個則是序列到序列翻譯（sequence to sequence translation），包括將語音轉為文字或翻譯不同語言。前者大多是利用卷積神經網路（convolutional neural networks，CNN）所完成，後者則多利用遞歸神經網路（recurrent neural networks，RNN），尤其是長短期記憶模型（long short-term memory，LSTM）。

晚餐要吃什麼

為了理解 LSTM 的運作原理，我們可以考慮一下「晚餐要吃什麼」這個問題：假設讀者住在公寓，很幸運地有個愛煮晚餐的室友。每天晚上室友都會準備壽司、鬆餅或披薩，而你希望能預測某個晚上你會吃什麼，並藉此規劃其他晚餐。為了預測晚餐，讀者建了一個神經網路模型。這個模型的輸入資料包括星期幾、第幾個月、以及室友是否開會開到很晚等會影響晚餐的因素。

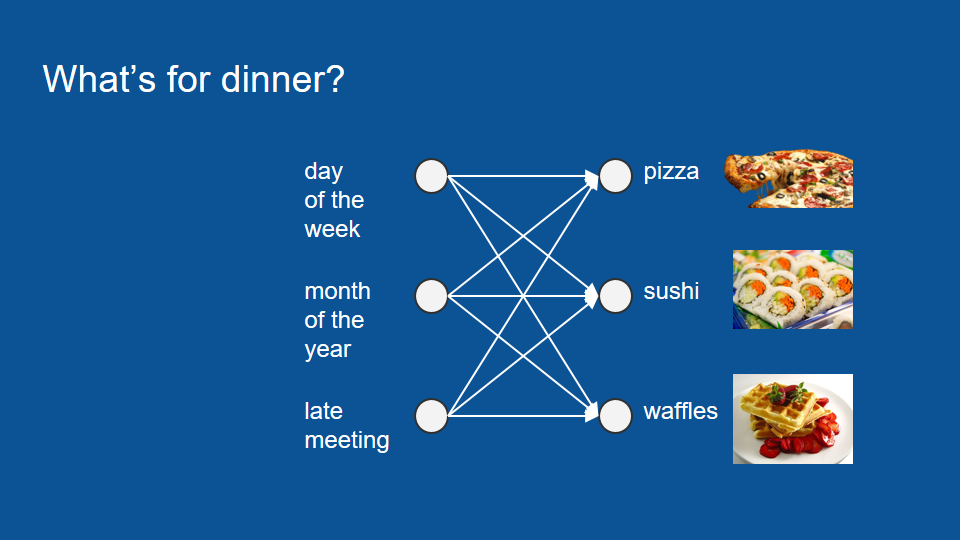
講到這裡，如果讀者對神經網路還不熟悉，可以花一點時閱讀〈神經網路的運作原理〉。

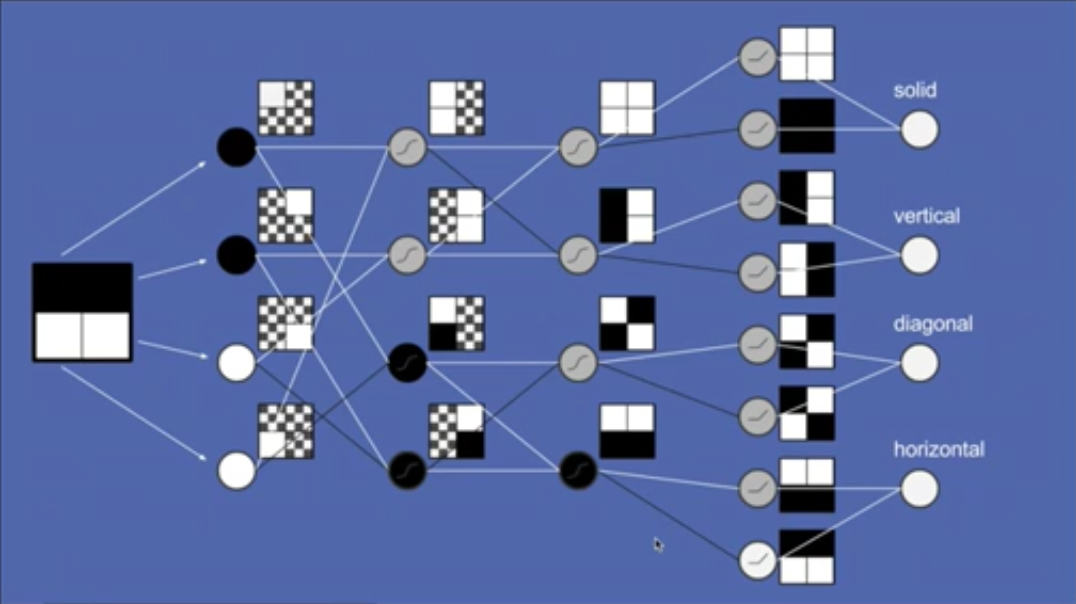
如果讀者想先跳過其他文章，又還不清楚神經網路是什麼，可以先把神經網路想成一個投票過程。神經網路裡包含了一個複雜的投票過程，而我們所輸入的資料，如星期幾、第幾個月等等，都會進入這個過程。接著我們可以根據過去的晚餐訓練這個模型，並預測今天的晚餐。

不過，用這種方法訓練的模型，表現並不是很好。就算我們謹慎挑選輸入資料並訓練模型，它的表現還是沒有比隨機猜測好上多少。

和其他複雜的機器學習問題一樣，先退一步回顧資料，可以幫助我們找出其中的規律。於是我們發現，原來室友在做完披薩後的隔天會準備壽司，再隔一天會準備鬆餅，然後又回去做披薩，就這樣持續下去。由於這個循環很普通，跟星期幾沒什麼關係，我們可以根據這項特徵訓練一個新的神經網路模型。

在這個新的模型裡，唯一重要的因素只有昨天吃過的晚餐，所以如果昨天吃披薩，今天就會吃壽司；昨天吃壽司，今天吃鬆餅；昨天吃鬆餅，今天吃披薩。整個投票過程變得非常簡單，預測也很準確，因為你的室友做事非常連貫。

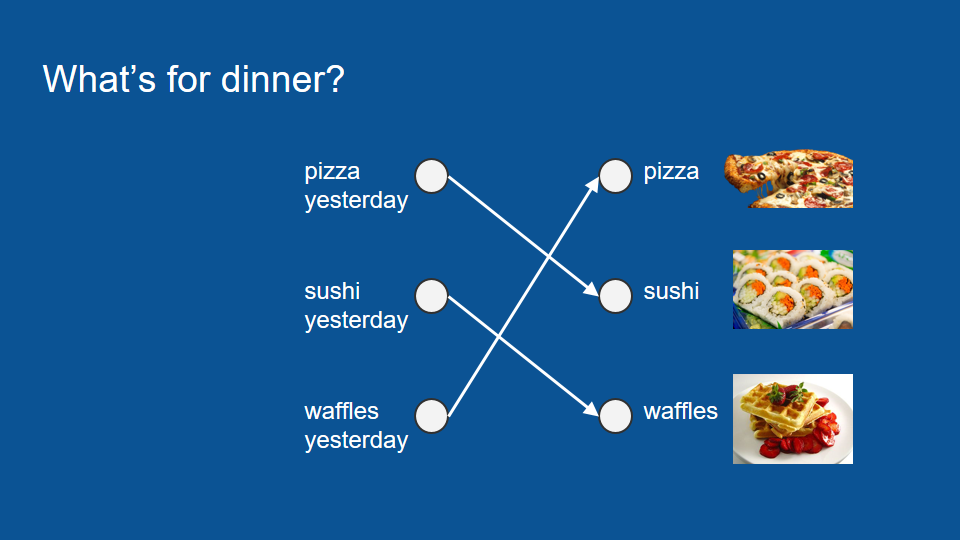
現在考慮另一個情況：如果讀者有某一晚不在家，像是昨天晚上出門了，那就無從得知昨天晚餐吃什麼。不過，我們還是能從幾天前的晚餐推測今天會吃什麼——只要先從更早之前推回昨天的晚餐，就能接著預測今天的晚餐。

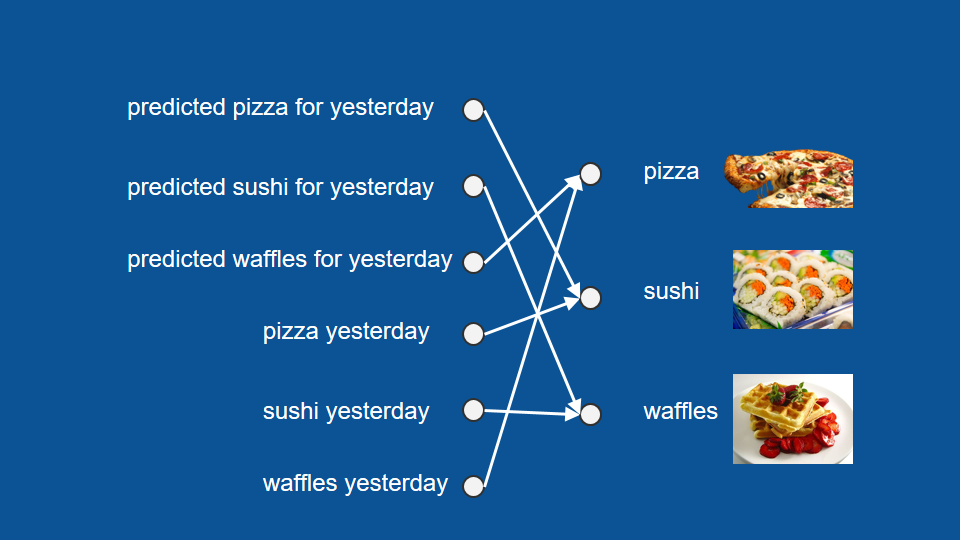
總之，我們不只能利用昨晚實際吃什麼，也能利用昨晚的預測結果。

向量和 one-hot 編碼

講到這裡，我們可以先岔開談一談什麼是向量（vector）。向量只是用來表示一組數字的數學名詞。如果我想描述某一天的天氣，我可以說當天的最高溫是華氏 76 度（約攝氏 24.5 度），最低溫是 43 度（約攝氏 6 度），風速是每小時 13 英里（約 21 公里），而且降下 0.25 吋（約 6.4 公釐）雨量的機率是 83%。

這就是所謂的向量。向量，也就是一組數字，之所以方便，在於它是電腦原生的語言。如果讀者想將資料轉成電腦能夠運算、處理、並能應用機器學習的形式，一組數字即為正確選擇。所以任何資訊在經過演算法處理前，都會先被轉換成一組數字。就連「今天是週二」這個概念，我們也可以利用向量表示。

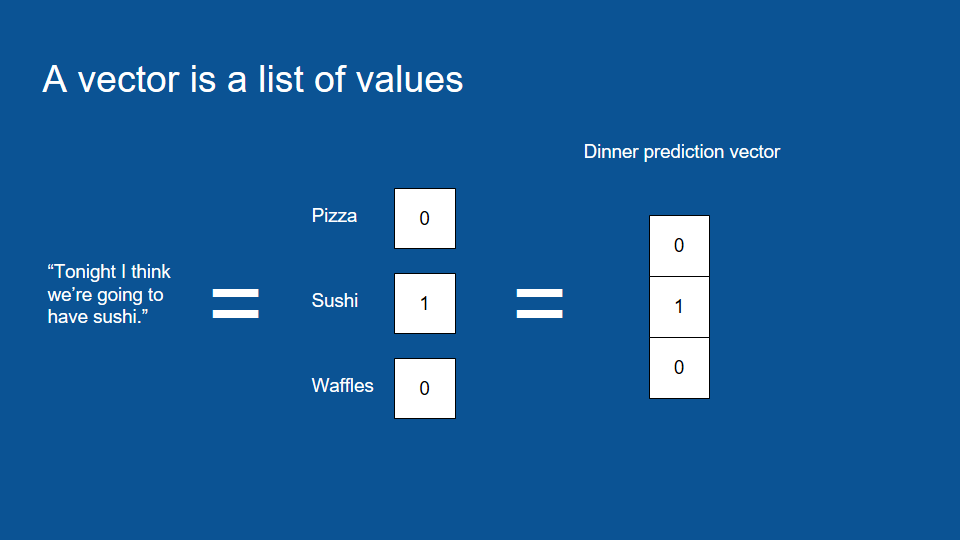
要表達這類的資訊，我們只要先在向量中包含所有可能的值，也就是週一到週日，再為每個值賦予特定的數字，將週二設為 1（Boolean True），其他日子設為 0（Boolean False）。這種格式被稱作 one-hot 編碼（或譯作「獨熱編碼」），而這種包含一連串 0、只有一個 1 的向量在資料分析中也很常見。

雖然 one-hot 編碼看起來很沒效率，實際上這能幫助電腦更簡單地處理資訊，所以我們可以將「今天晚餐吃甚麼」的預測轉換成一個 one-hot 向量，將預測結果之外的數值都設為 0。在下圖的例子裡，我們預測的晚餐是壽司。

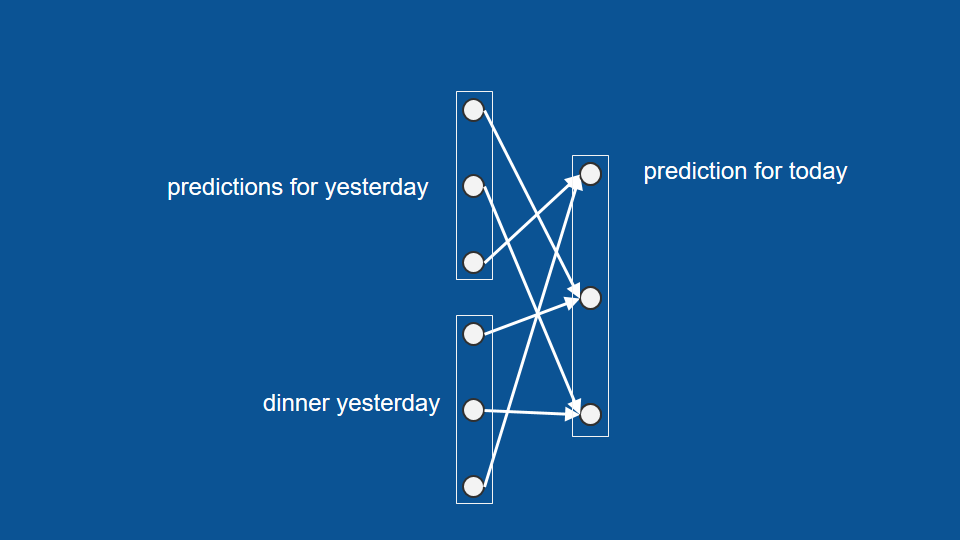
現在我們可以將所有的輸入和輸出組合成幾個向量，也就是幾組數字。這可以幫助我們解釋整個神經網路的架構。利用我們歸納出的三個向量：昨天的預測、昨天的結果、以及今天的預測，這裡的神經網路架構即為每個輸入因素和輸出因素間的關聯（connection）。

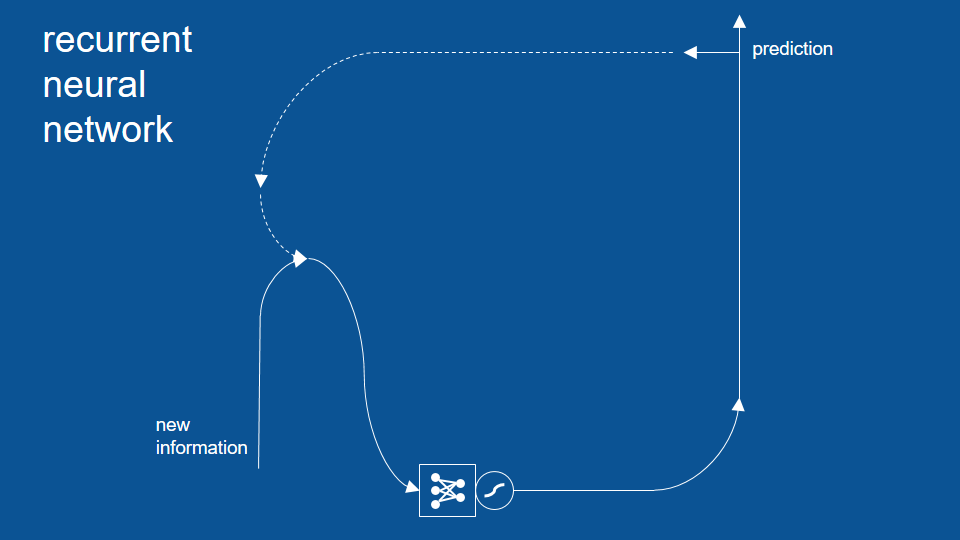
為了完成上面的示意圖，我們可以加上今日預測結果的回收循環。下圖中的虛線，表示了今天的預測結果如何在明天被重新利用，成為明天的「昨日預測」。

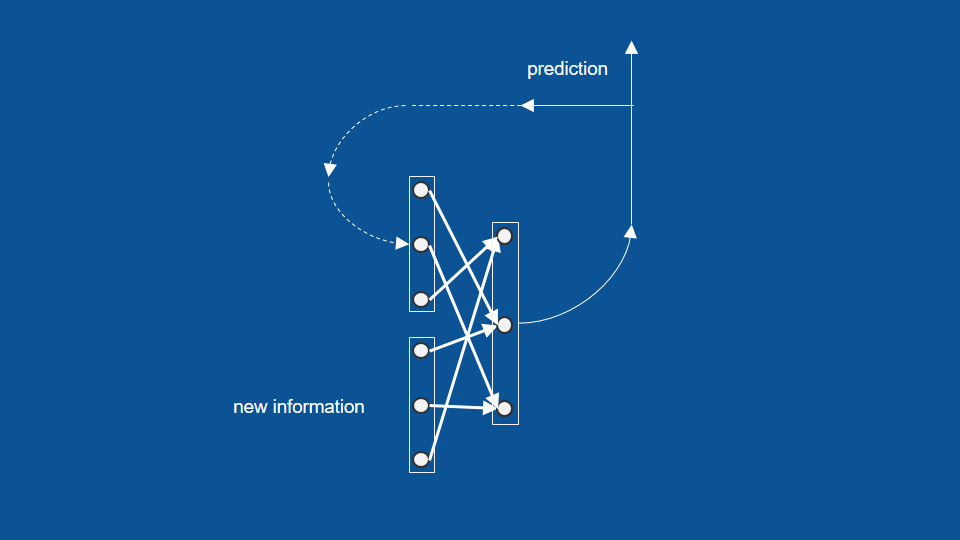
這個模型也說明了為什麼我們在缺少某些資訊的情況下（例如不在家兩週），還是能準確預測今晚吃甚麼。只要忽略接收新資訊的部分，我們就能將紀錄時間和餐點的向量延伸到最近的資料點，並接著預測下去。

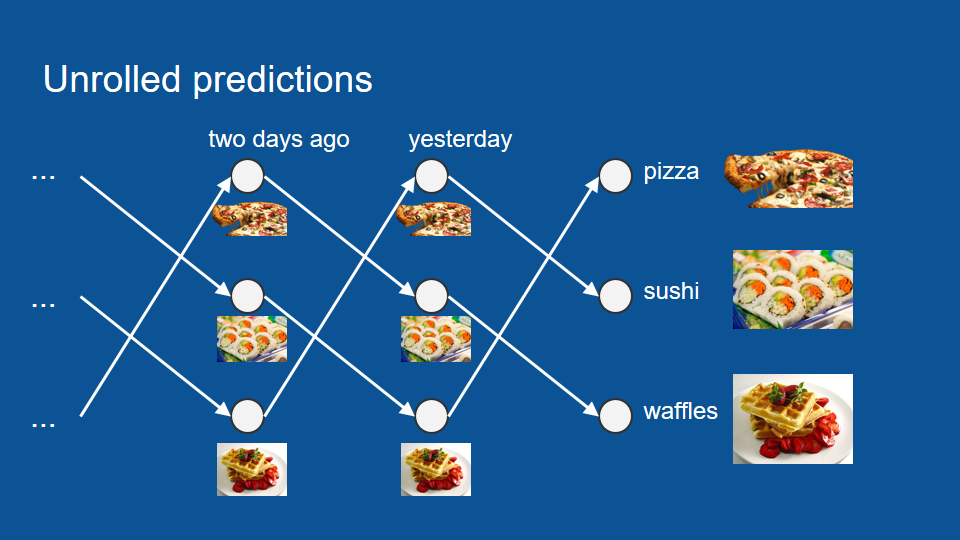
延伸過後的神經網路如下圖所示。我們可以從最前端一直往過去的資料延伸，看更早之前的晚餐是甚麼，再往兩週的空缺延伸，直到我們得到今晚的預測。

寫一本童書

以上就是一個理解 RNN 運作原理的好例子。不過為了突顯這個模型的限制，我們可以換一個寫童書的例子。這本童書裡只有三種句子：「道格看見珍（句號）」、「珍看見小點（句號）」、以及「小點看見道格（句號）」。

這本童書的字彙量很小，只有「道格」、「珍」、「小點」、「看見」以及句號。在這個例子裡，神經網路的功用在於將這些單字按正確的順序排好，完成一本童書。我們先將前面的晚餐向量，換成這個例子裡的字典向量。

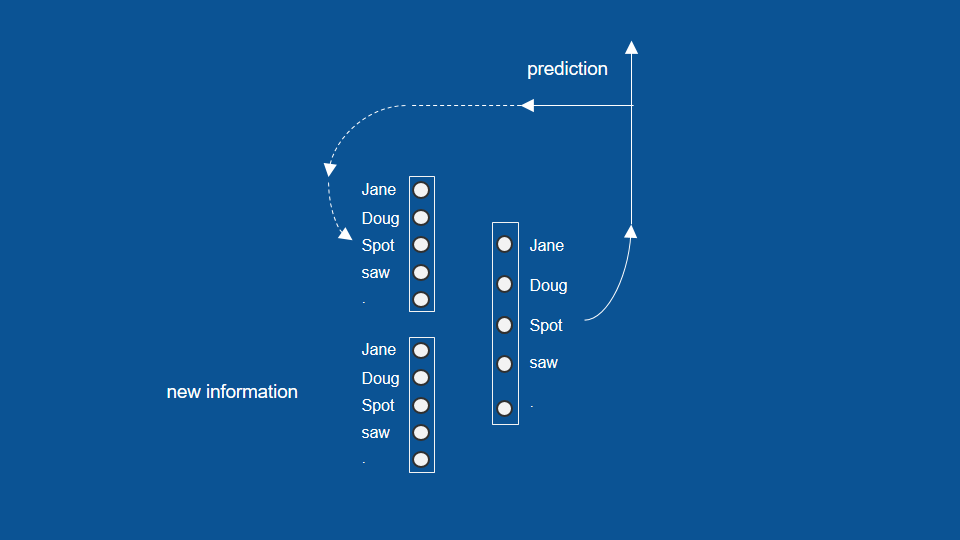
接著我們就能用前面的方法（即 one-hot）表達不同單字。如果道格是我最後讀到的單字，那我的資訊向量中，就只有道格的數值為 1，其他的數值都為 0。我們也可以按前面的方法，利用昨天（前一次）的預測結果，繼續預測明天（下一次）的結果。經過一定的訓練後，我們應該能從模型中看出一些特定的規律。像是在「珍、道格、小點」之後，模型預測「看見」和句點的機率應該會大幅提升，因為這兩個單字都會跟著特定名字出現。

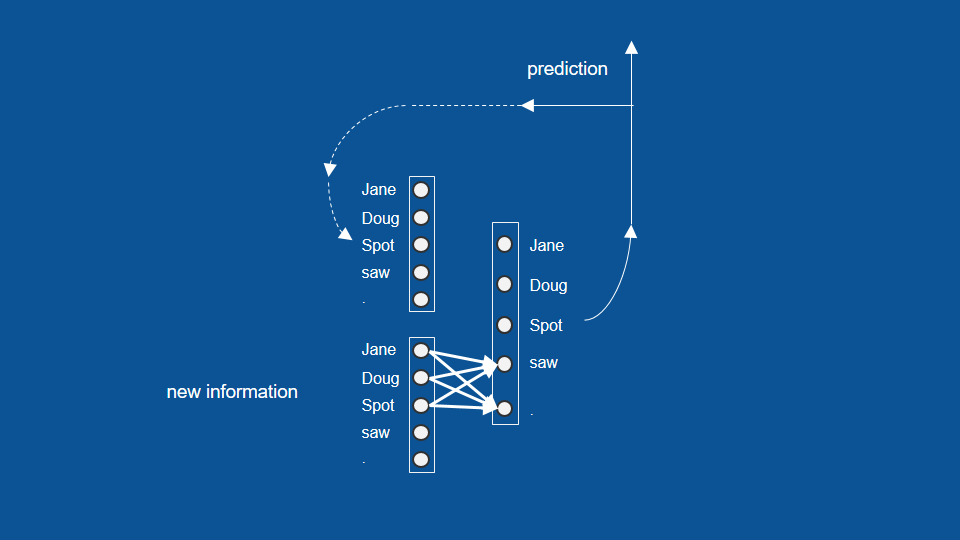
同樣地，如果我們前一次預測了名字，那這些預測也會加強接下來預測「看見」或句號的機率；如果我們看到「看見」或句號，也能想像模型接下來會傾向於預測「珍、道格、小點」等名字。

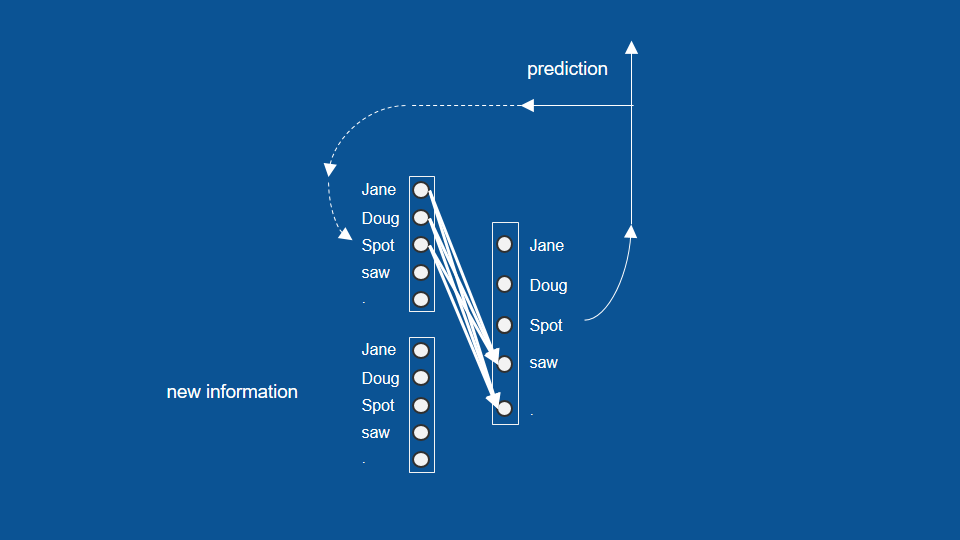
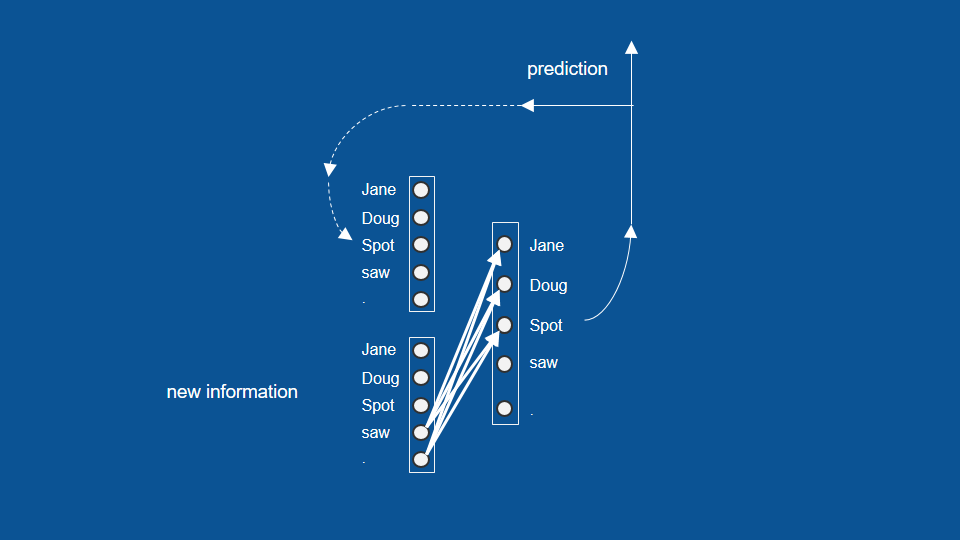
於是，我們可以將這個流程和架構視為一個 RNN 模型。為了簡單起見，這裡我將向量和投票權重用一個包含點和線（箭頭）的符號代替。

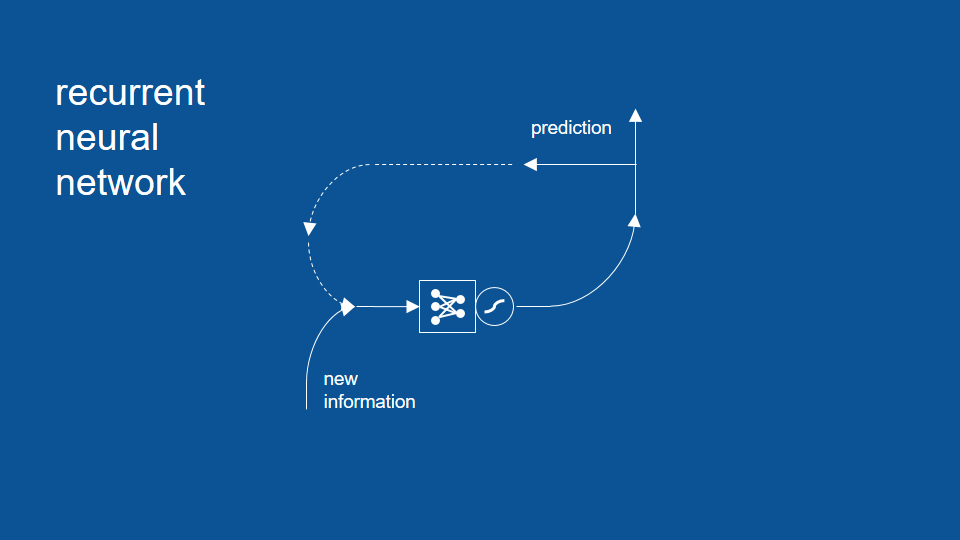
擠壓函數（雙曲正切函數）

除了模型本身，這張圖還包括了一個我們前面沒提到的符號。這個波浪符號代表擠壓函數（squashing function，又譯作 S 函數），它可以幫助整個神經網路更好運作。

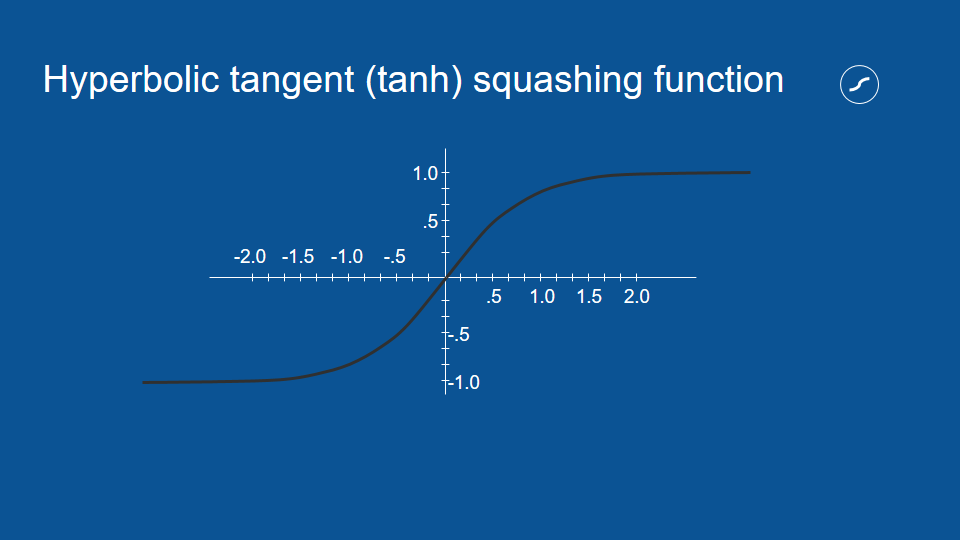
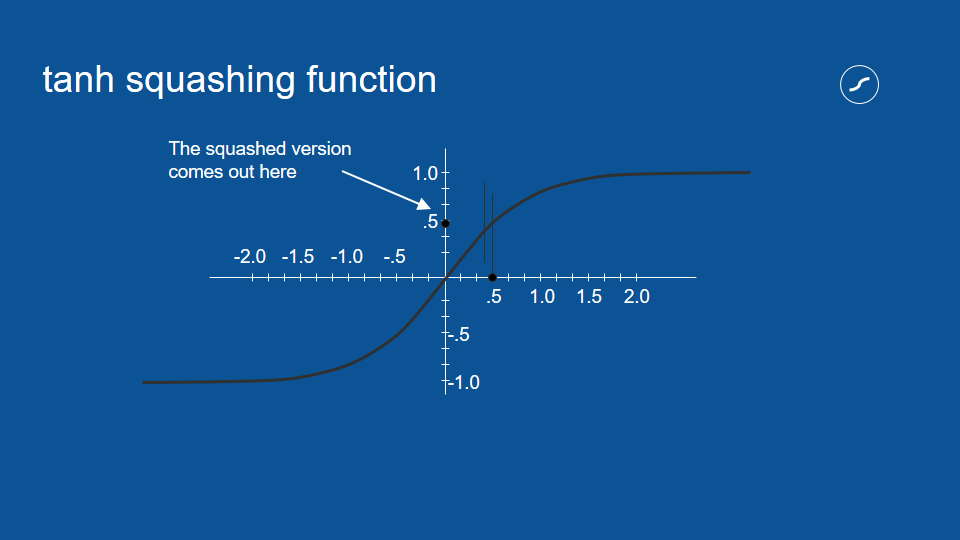
擠壓函數的功用，是將模型的投票結果限制在特定範圍之間。比方說，如果有個投票結果得到 0.5 的值，我們可以在擠壓函數上畫一條 x = 0.5 的垂直線，並得到水平對應的 y 值，也就是擠壓過後的數值。

對於小的數值而言，原始數值和擠壓過構的數值通常很相近，但隨著數值增大，擠壓過後的數值會越來越接近 1。隨著數值愈趨負無窮大，擠壓過後的數值也會越來越接近 -1。不論如何，擠壓過後的數值都會介於 1 和 -1 之間。

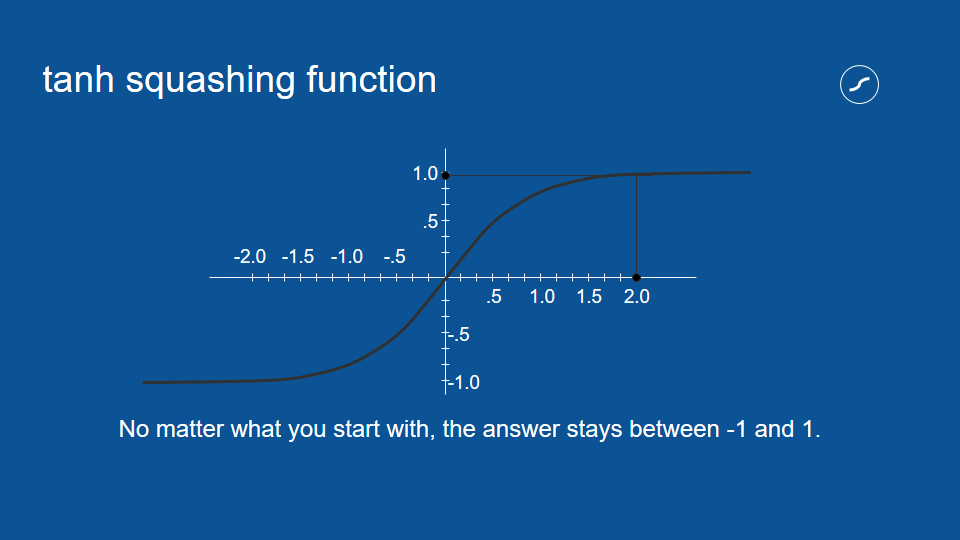
擠壓函數的處理，對於神經網路這種重複運算相同數值的流程非常有用。比方說，如果有個選項每次都得到兩次投票，它的數值也會被乘以二，隨著流程重複，這個數字很容易被放大成天文數字。藉由確保數值介於 1 和 -1 之間，即使我們將數值相乘無數次，也不用擔心它會在循環中無限增大。這是一種負回饋（negative feedback）或衰減回饋（attenuating feedback）的例子。

可能出現的錯誤

讀者可能已經注意到，這個例子裡的神經網路會出現一些錯誤，像是得出「道格看見道格（句號）」等句子，因為每當「看見」出現在模型裡，後面接著名字的機率就會大幅提升。當然，我們也可能得到「道格看見珍看見小點看見道格」之類的錯誤。

這是因為我們的模型有著很短期的記憶，只會參考前一步的結果，所以它不會參考更早之前的資訊，以避免這類錯誤。為了解決這個問題，我們需要在模型中加入更多內容。

記憶／遺忘路徑

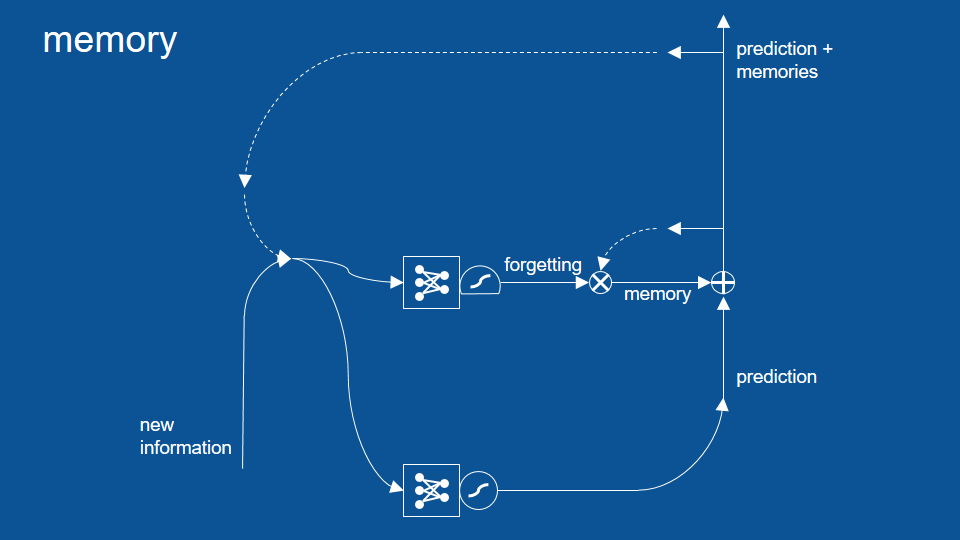
上圖中，我們新增的關鍵是記憶／遺忘（memory and forgetting）路徑，用於幫助模型能記住幾個循環前發生的事情。為了解釋記憶部分的運作原理，我們需要先認識幾個新的符號。

逐元素相加、相乘和閘門

首先，圈圈裡包含十字的符號是（矩陣）逐元素加法（element by element addition）。它的運作原理是將兩個相同長度的矩陣按同位置和順序的元素相加，所以我們可以將第一個向量中的第一個元素，和第二個向量中的第一個元素相加，得到輸出向量中的第一個元素。

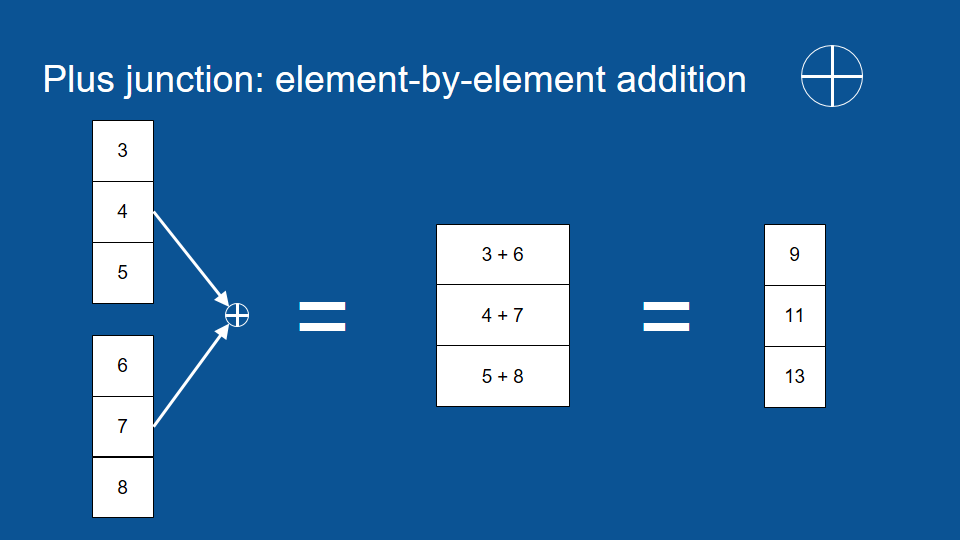
於是在上圖中我們可以看到 3 加 6 等於 9。我們可以接著處理下一個元素：4 加 7 等於 11，最後我們所得到的向量會和原本長度一樣，不過其中每一個元素都是前兩個向量逐元素的和。

相信讀者也能猜到圈圈裡有個交叉的符號是（矩陣）逐元素乘法（element by element multiplication）。它和逐元素加法的運作原理類似，只是運算方法從加法換成了乘法。

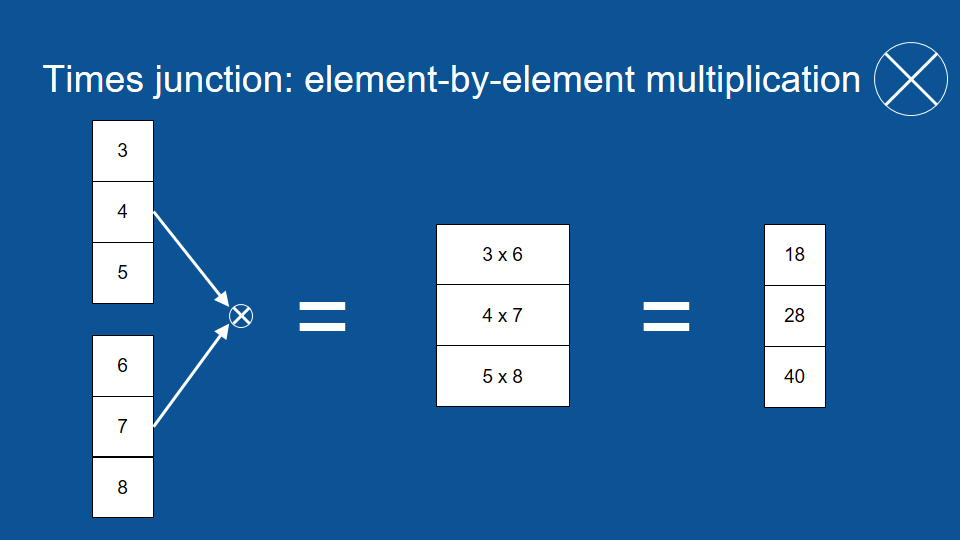
逐元素相乘可以幫助我們完成一些很酷的事情。我們可以想像有一組訊號，以及一組可以控制水量的水管。在這個例子裡，我們把初始訊號都當作 0.8。

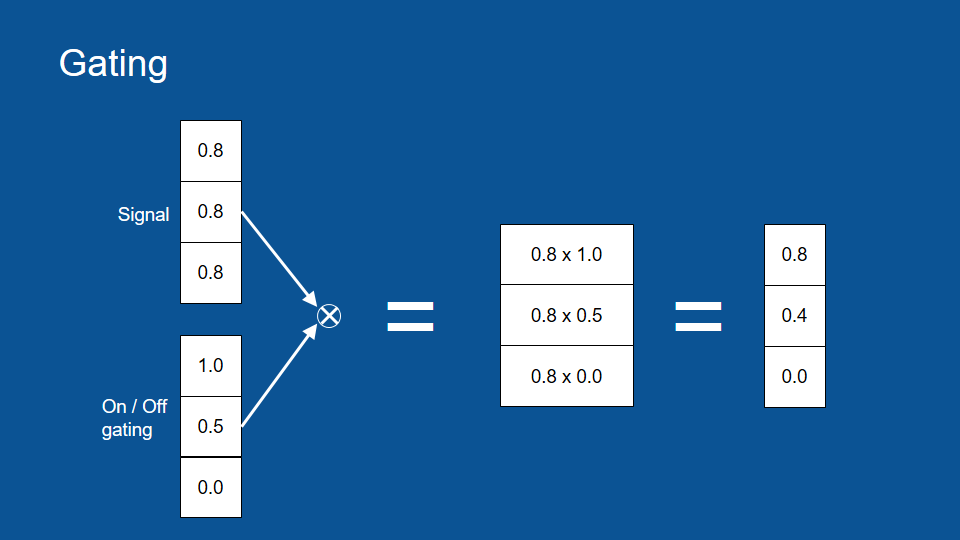
在每個水管上都有一個龍頭，可以用來全開、全關或任意水量，讓訊號流通或堵塞。所以在這個例子裡，全開的龍頭有乘數 1，而全關的龍頭則有乘數 0。根據前面提到的逐元素乘法，我們可以在一開始將 0.8 乘上全開的 1，得到原本的訊號 0.8，也會在最後將 0.8 乘上 0，得到被遮蔽的訊號 0。中間的 0.8 則會乘上 0.5，得到一個比較小、衰減過後的訊號。這組閘門（gate）可以讓我們控制訊號的流通與否，非常有用。

擠壓函數（邏輯函數）

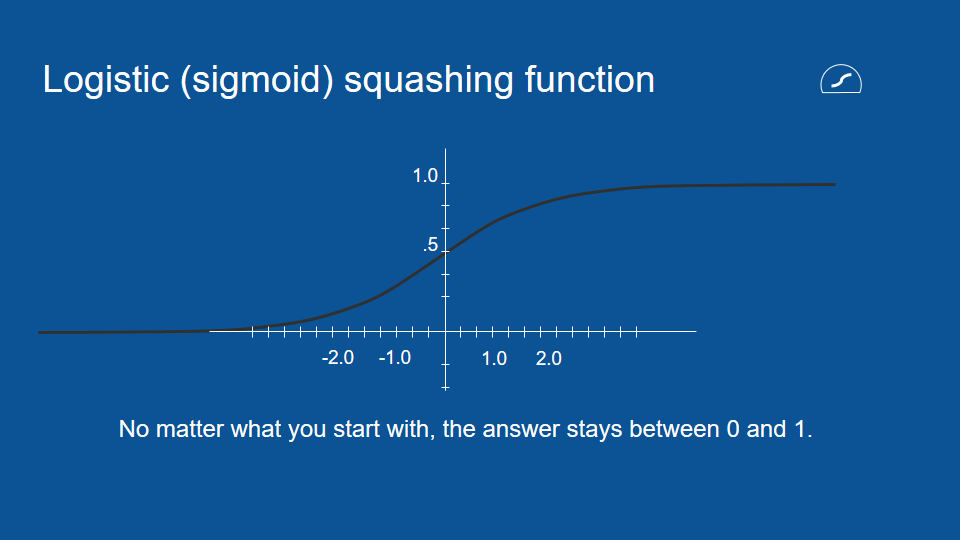
為了實現上述的閘門，我們需要一組介於 0 和 1 之間的數值，所以這裡又有另一種壓縮函數。這個函數的符號是一個帶有平底的圓形，它被稱作邏輯函數（logistic function）。邏輯函數和我們前面提到的雙曲正切函數（hyperbolic tangent function）很類似，除了前者的輸出值介於 0 和 1 之間，而非後者的 -1 和 1 之間。

介紹完這些新名詞之後，在新的模型裡，我們還是會利用先前的預測（昨天的預測）以及新的資訊（昨天的結果）。我們會利用兩者作出新的預測，而這些新的預測會在下一次循環回模型當中。

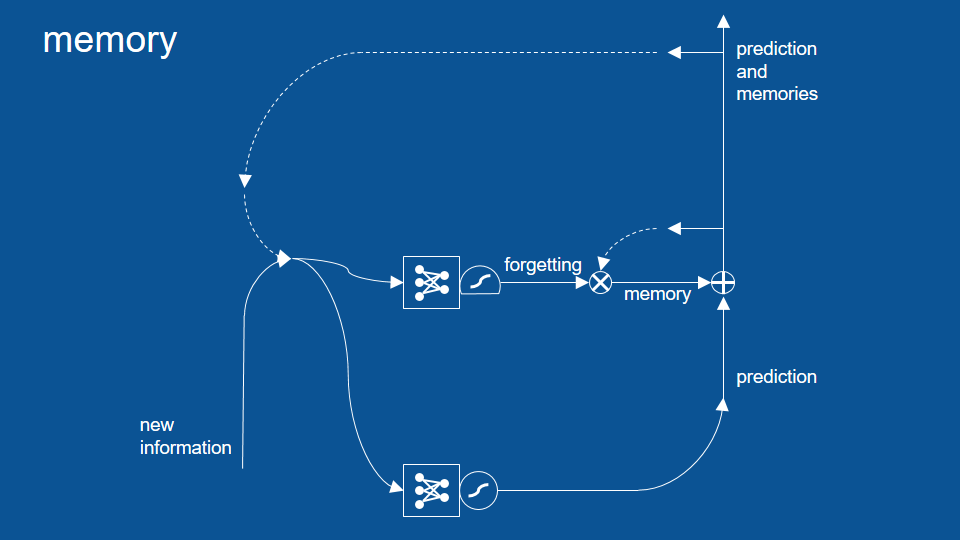
不過在新的模型裡，這些新預測會通過下圖中的新路徑。在這條路徑裡，我們會透過邏輯函數，建立一個回憶或遺忘特定資訊的閘門（即圖中的「圈叉」符號），並將結果加回下次的預測當中（即圖中的「圈加」符號）。

篩選路徑

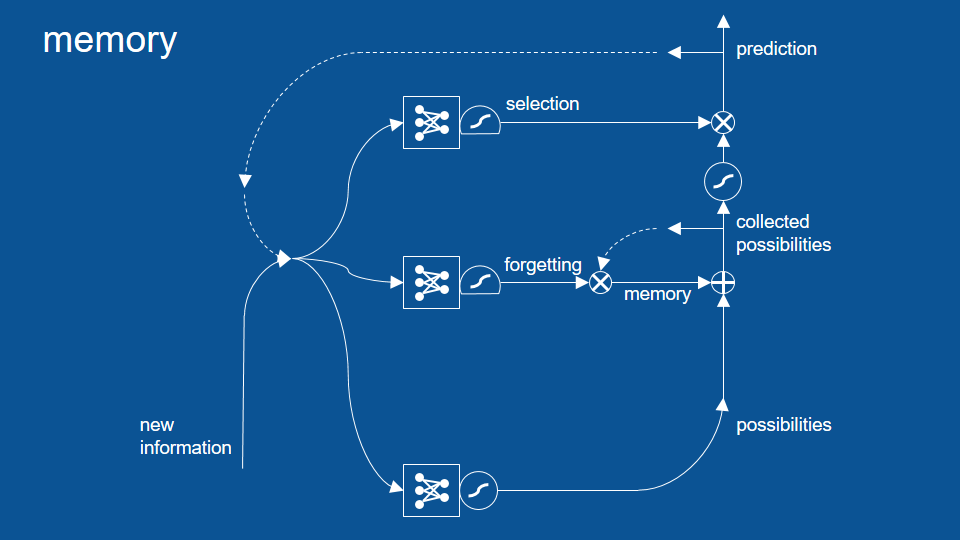
在這個新的循環裡，我們不只有預測，而是由回憶篩選過的預測，這些回憶中包含了長久下來模型並未遺忘的資訊。於是這邊多了一組完全獨立、用於記得和遺忘資訊的神經網路。新增的遺忘路徑可以幫助我們保留任意時間長短的資訊。

這時讀者可能會發現在結合了預測和回憶之後，我們不一定會直接將這組結果當作最終的預測。所以模型中最後還加上了一個篩選（selection）路徑，將一部分的預測結果保留在模型中。

這個篩選路徑也自成一個神經網路，有自己的投票機制。所以每次循環一開始的新資訊和舊預測，也會用於決定篩選路徑中的閘門大小。這組閘門會決定哪些結果該留在模型中，哪些結果該作為最終預測。

在篩選路徑前，我們可以看到另一個壓縮函數。因為在這之前我們做了一次逐元素相加（即圖中的「圈加」符號），預測結果可能會比 1 大或比 -1 小，所以這邊的壓縮函數是用來確保數值大小尚在控制範圍中。

於是在上圖中我們可以看到，每當新預測，也就是一組預測結果（possibilities）產生時，我們會將它和過去的回憶結合，並將從中選出特定幾項作為該次循環的預測結果。在這個循環中，每條路徑中的機制都是透過神經網路學習，包括何時該遺忘或將回憶刪除。

忽視路徑

最後在完成整個模型前，我們還需要加上另一組閘門。新增的忽視（ignoring）路徑可以幫助我們篩選掉初步的預測結果。這項機制是故意的，讓近期內不是很相關的結果先被忽視，避免它們影響之後的路徑。和其他路徑一樣，忽視路徑有自己的神經網路、邏輯擠壓函數和閘門（即圖中右下角的「圈叉」符號）。

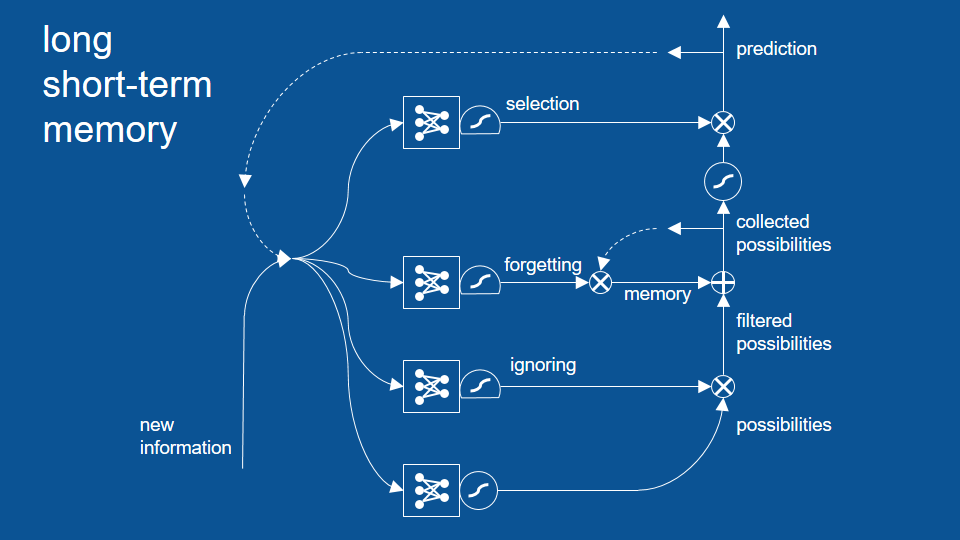
「珍看見小點（句號），道格⋯⋯」

到目前為止，LSTM 模型裡已經有了許多組成部分，相信讀者一時之間也摸不著頭緒，所以我們可以透過一個很簡單的例子了解整個模型如何運作。這確實是一個過度簡化的例子，等一下歡迎糾正我，不過當讀者能找出這些問題時，也代表你們能接著學習更高階的內容了。

我們先回到一開始提到的寫童書的例子，並為了簡單起見，我們可以假設整個 LSTM 模型已經被訓練完畢，也就是說模型裡的投票機制和權重都已經底定了。以下利用逐頁動畫說明。

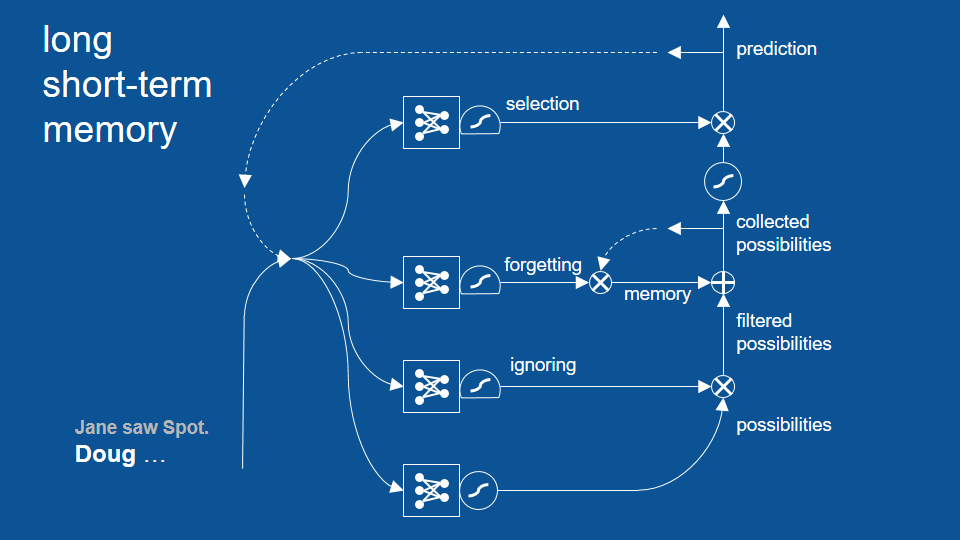
我們的故事到目前為止是「珍看見小點（句號），道格⋯⋯」。「道格」成了目前故事裡的最後一個字，而且不意外地，前一次的預測結果包含了「道格、珍、小點」等名字。這是因為先前我們用句號結束了上個句子，所以下個句子可以用任何名字開頭。

於是我們有了新資訊「道格」，以及上次的預測「道格、珍、小點」。我們接著將這兩組向量輸入包含預測、忽視、遺忘和篩選等四條路徑的模型中。

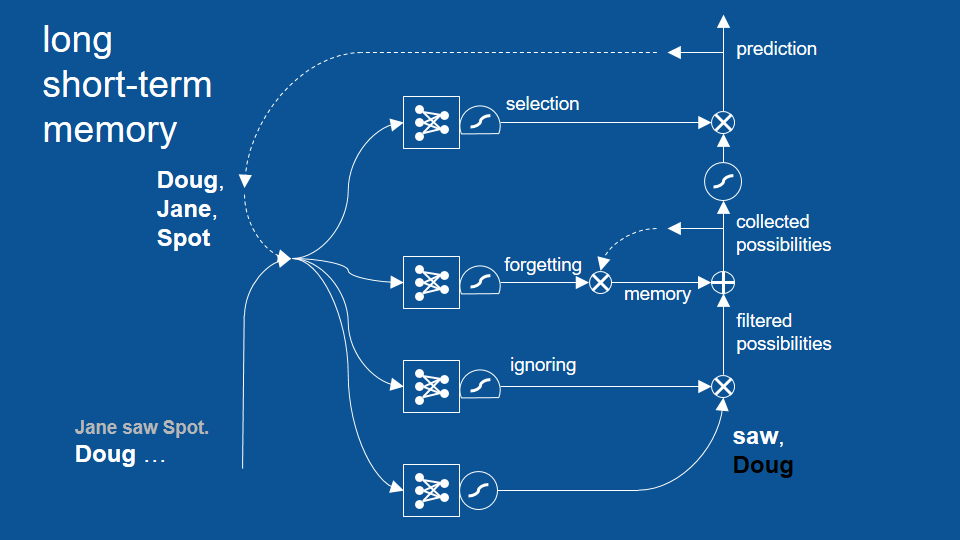
模型中的第一步是先做出預測。由於「道格」是故事裡的最後一個字，這個步驟可以判斷接下來出現「看見」的機率很高，也會判斷短期內不該再出現「道格」。所以路徑最後會產出「看見」的正預測（positive prediction）和「道格」的負預測（negative prediction）。由於我們並不預期短時間內「道格」會再次出現，上圖預測路徑中的「道格」以黑字表示（即「非道格」）。

接著，在這個簡單的例子裡，我們可以不用考慮忽視路徑，於是這組結果會進一步通過回憶路徑。同樣地，為了簡單起見，我們就當作這個模型裡還沒有任何回憶，所以預測結果又直接進到了篩選路徑。

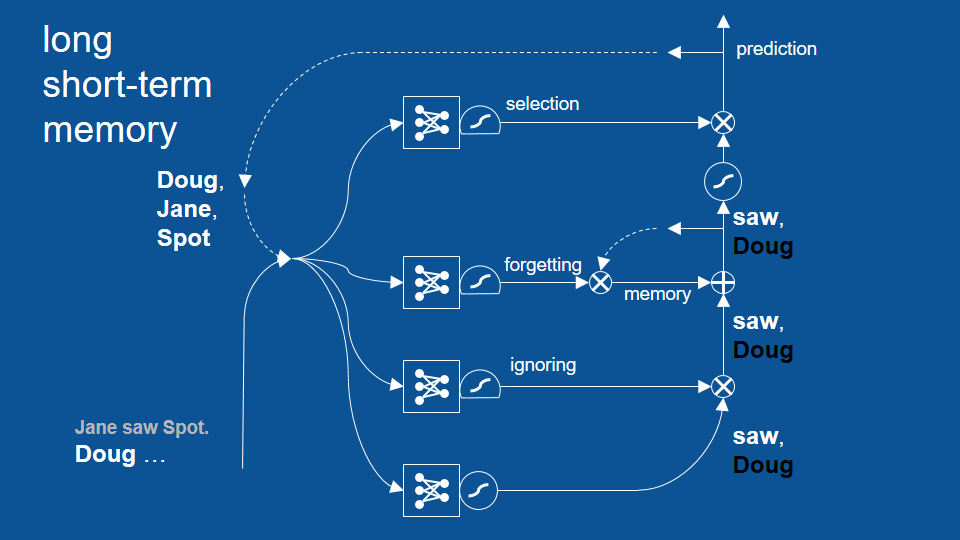
由於篩選機制已經學習了「在前一個單字是名字的狀況下，接下來的結果只能是『看見』或句號」這項規則，於是「非道格」這項預測就被擋掉了，剩下「看見」成為最終預測。

我們可以接著利用這個結果，開始下一個預測循環。在新的循環裡，「看見」同時是新資訊和舊預測，並和前一次循環一樣，走過四條路徑並形成新的預測。

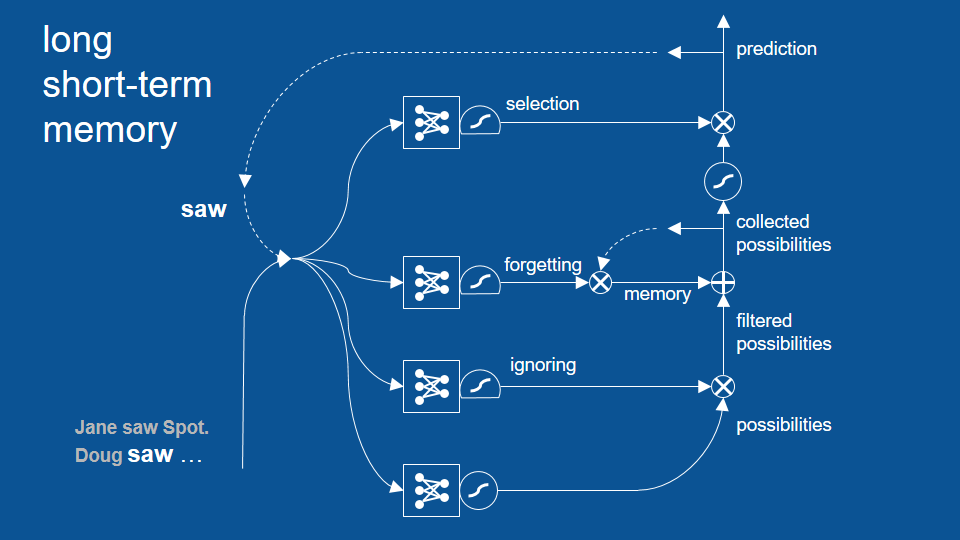
由於「看見」才剛出現，我們預測下個字應該是「道格、珍、小點」其中之一。同樣地，在這個簡單的例子裡我們可以先跳過忽視路徑，並讓這三個預測進入下個路徑。

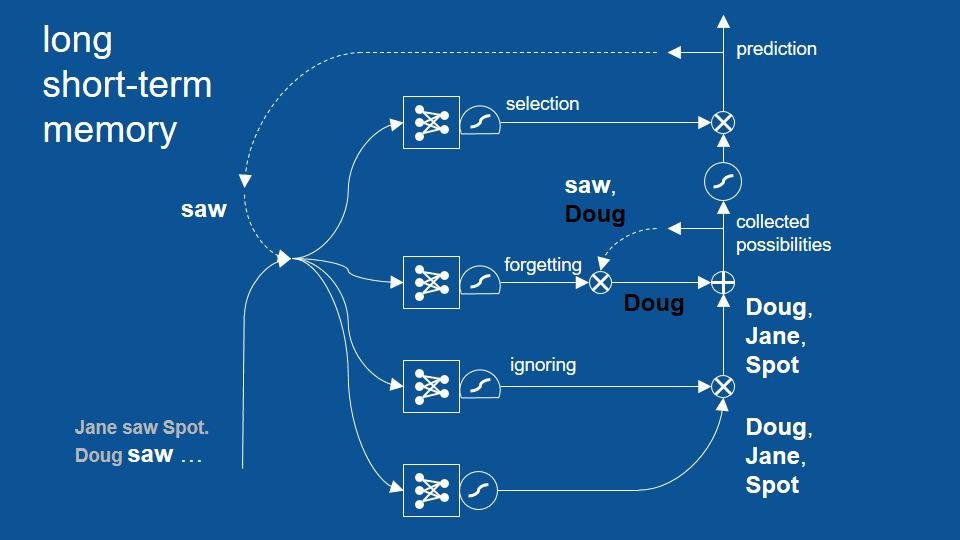
這個路徑也包括我們前一循環的預測結果，也就是「非道格」和「看見」。它們在前一回合中被保留了下來，並進到了遺忘閘門。

這時遺忘閘門的思路是：「嘿，既然前一個單字是『看見』，根據經驗我可以將回憶中的『看見』忘掉，保留名字就好。」於是這條路經將前一次預測（看見、非道格）中的「看見」給忘了，並接著將「非道格」加入了初步的預測結果（道格、珍、小點）當中。

最後在這條路徑裡，「道格」的預測正負抵消，只留下了「珍」和「小點」繼續前往下條路徑。

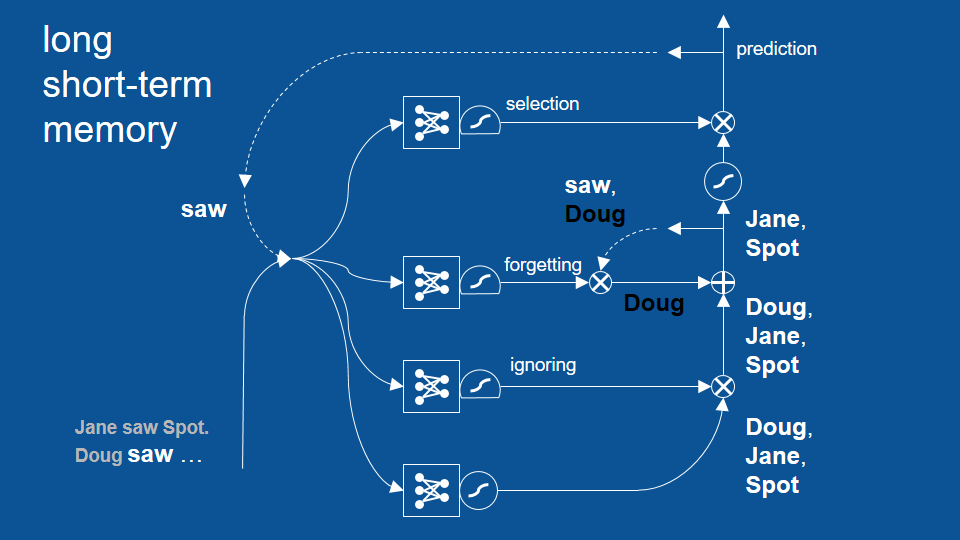
這裡的篩選閘門已經知道當「看見」是前一個單字時，下個出現的單字應該是一個名字，所以它讓「珍」和「小點」雙雙通過。

於是，在最後的預測結果中，我們得到了「珍」和「小點」，但沒有「道格」。

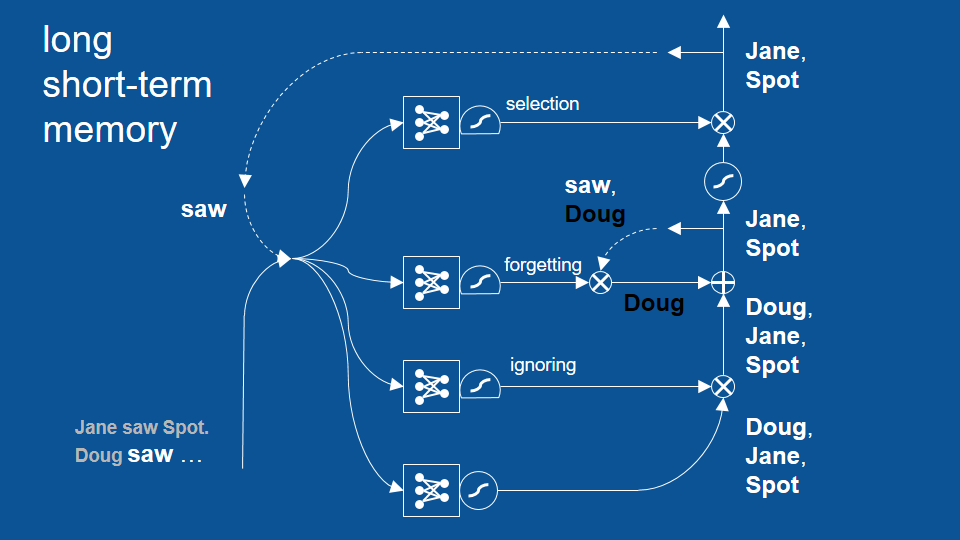
LSTM 的其他應用

這個循環成功避免了先前「道格看見道格」的錯誤，並展示了 LSTM 模型如何藉著回顧兩個、三個甚至更多循環前的結果，以作出更合理的預測。不過話說回來，其實先前的基礎 RNN 也能回顧幾個循環前的結果，只是沒有 LSTM 這麼多。LSTM 可以成功回顧更多循環前的結果。

LSTM 模型對許多特別實用的應用來說很有幫助。例如，如果我想將某段話從一個語言翻譯成另一個語言，LSTM 的表現相當良好。儘管翻譯並非逐字、而是逐詞組處理的過程，有時甚至是逐句，LSTM 可以表現出某個語言中的文法架構。在以上說明的路徑和步驟中，LSTM 模型似乎能捕捉某些更高層次的規則，並根據這些規則翻譯不同語言。

另外 LSTM 也很擅長將語音轉換為文字。由於語音指示隨著時間變化的訊號，LSTM 可以利用這些訊號預測文字，並根據文字出現的次序更好地判斷接下來的文字。LSTM 也因此擅長於任何和時間有關的資訊，包括音訊、影片，以及我最喜歡的機器人學（robotics）。由於機器人學基本上只是探討代理個體（agent）根據一連串感測而得的資訊所作出的判斷和動作，這類資料本身就帶有序列性（sequential），即不同時間內所採取的動作，也和之後的感測與判斷有關。

如果讀者還對 LSTM 的數學表達方式有興趣，以下是 Wikipedia 上的介紹。

雖然我不會詳細介紹這些算式，但我鼓勵讀者可以體會一下這些看似複雜的算式，是如何勾勒出以上這個還滿直觀的流程。如果讀者想了解更多，我也鼓勵閱讀你們讀完 Wikipedia 上的介紹，並參考以下的討論和教學。這些 LSTM 的解釋應該也對讀者很有幫助。

遞歸神經網路和長短期記憶模型 RNN & LSTM